算数オリンピック
2022年大会　表彰者からのメッセージ

友人が参加していたので、今回も参加することにしました。

表彰式に行けるのが嬉しかったです。

表彰式の会場で、入賞者と話せたのが良かったです。特に遠いところに住んでいる方とはなかなか話せる機会がなかったので良い機会でした。数学の話で盛り上がりました。

ピーターフランクル先生の講演で、小学生の方々がたくさん手を挙げて、分かりやすく問題の解き方を解説するのを見て、日本の未来は明るいなぁと思いました。

問題2 II - (2)

問題文がシンプルでありながら、桁数の和というのは今まで見たことがなかったので、最初本当に答えが求められるのかと意表を突かれました。好きです。

問題4

そこに正三角形が出てくる問題は初めて見ました。新鮮な気持ちで取り組めました。

下手の横好きですが、将棋が好きです。去年友人に誘われて始めました。
食べ物だと、焼きそばやそうめんが好きです。

数学は継続して勉強しています。数学の他には、競技プログラミングにハマっています。

学校の先輩方や先生方に多く尊敬している人がいます。

なにか数学と関わりのある仕事ができたらいいなと思っています。

パズルのような問題です。

Putnam 1979 A4

(和訳) 平面上にn個の赤い点と, n個の青い点があり、どの3点も同一直線上にありません。赤い点と青い点を結ぶn個の線分を、どの線分も互いに交わらないように書くことができるでしょうか？できるならその証明を、できないなら反例を示してください。

n=4 の場合の例

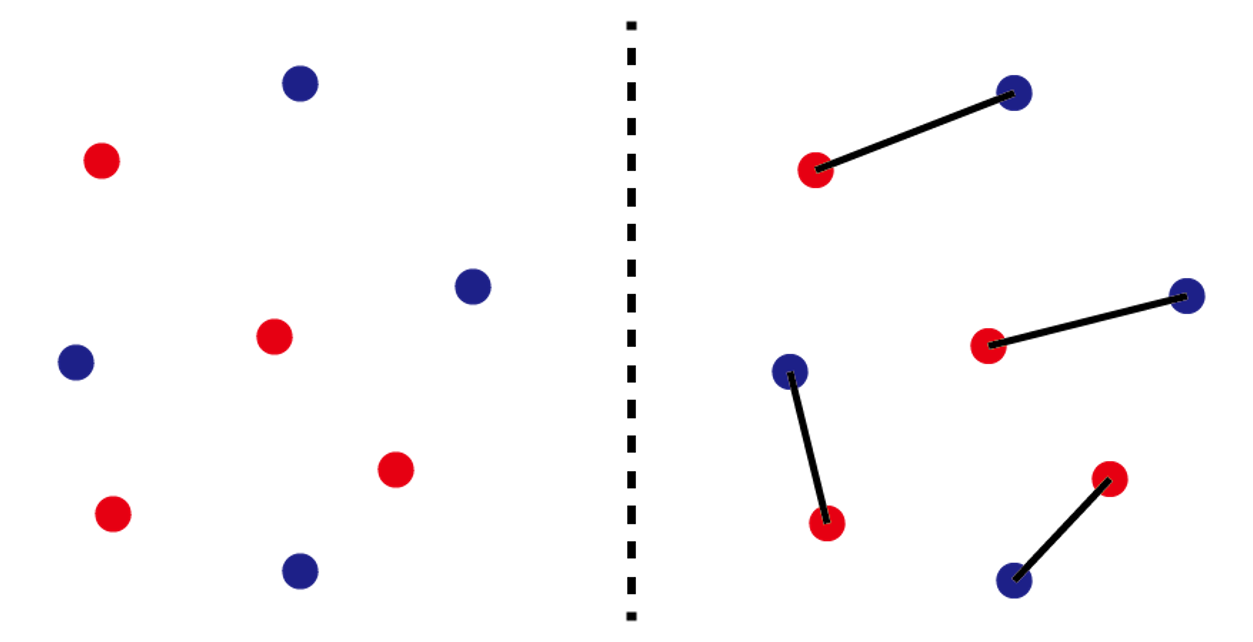
問題は簡単ですが、解こうとすると意外に難しいです。しかし、解法自体は小学生でも十分に理解できます。
自力で頑張って解きました。

(ヒント1)
できます。n個の線分を条件をみたすように書くアルゴリズムを考えてみましょう。

(ヒント2)
最初何も考えずに赤い点と青い点を結ぶn個の線分を書いてから、簡単な操作を繰り返して条件を満たすようにすることを考えます。どのような操作にすればよいでしょうか？

(ヒント3)
この操作を繰り返してどのような点の並び方についてもうまく行くのは、なぜでしょうか？
操作することで必ず減るが負にはならない「なにか」を探せば、背理法で示せます。

(略解)
どの線分も互いに交わらないように書くことができることを示します。
まず適当に、2n個の点すべてが線分の端点になるように、赤い点と青い点を結ぶn個の線分を書きます。「交わっている二個の線分について、端点を入れかえて交わらないようにする」操作を考えます。 この操作を有限回繰り返すことで、どの線分も互いに交わらないようにできることを示します。

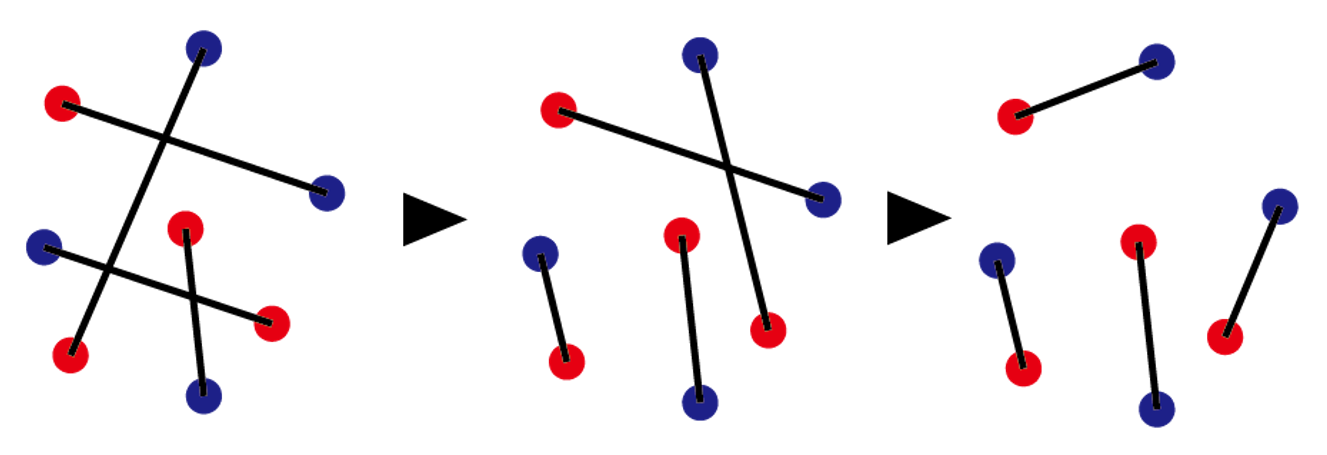
「操作するたびに線分の交点が必ず減るので、いつかは0になる」と思うかもしれません。私は最初そう思っていました。しかし、この方針は以下のような場合で成り立ちません。線分の交点が減るどころか増えてしまいます。

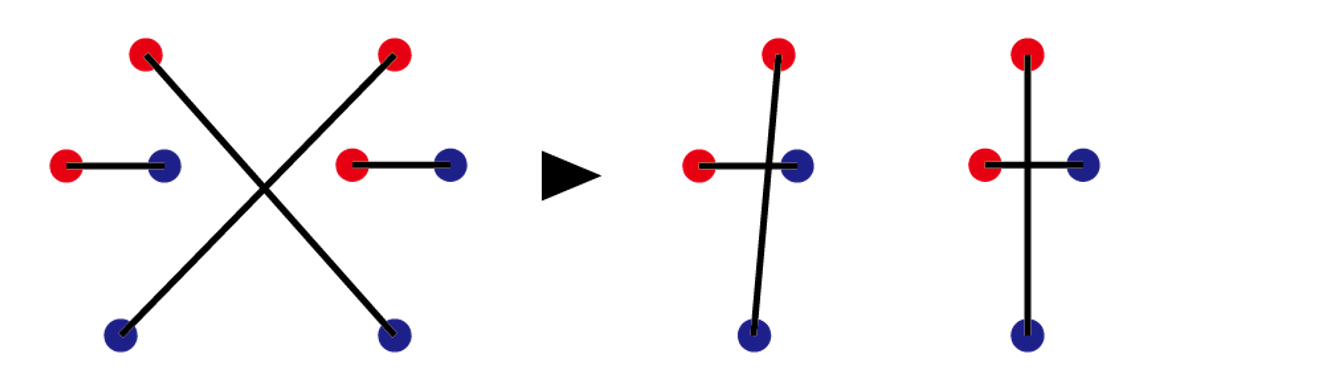
ここで、幾何の視点から考えてみます。 「操作するたびに線分の長さの和が必ず減る」ことが成り立つのです。
赤い点R1,R2と青い点B1,B2があり、線分R1B1とR2B2が交わっているとします。 操作すると線分R1B1とR2B2を消し、線分R1B2と R2B1を書くことになります。 ここで線分R1B1とR2B2の交点をXとすると

R1B1 + R2B2 = (R1X + B1X) + (R2X + B2X) = (R1X + B2X) + (R2X + B1X) > R1B2 + R2B1

よって操作するたびに線分の長さの和は減ります。ただし, 三角形の一辺の長さは、もう二辺の長さの和より小さいことを用いました。

背理法で示します。もしもどの線分も互いに交わらない線分の書き方が存在しないとすると、何回操作しても線分の長さの和が小さくなり、さらにいずれかの線分は交わります。つまり、線分の長さの和が異なるn個の線分の結び方をいくらでも作れることになるのです。しかし、2n個の点すべてが線分の端点になるような、赤い点と青い点を結ぶn個の線分の書き方は、高々有限個(n!個)です。よって、矛盾します。

どの線分も互いに交わらないように書くことができます。


線分の長さの和に注目するのが、意外です。最後の背理法を持ち出すところが綺麗ですね。