
算数オリンピックも「いいね!」
2023年中学入試問題を紹介!

<問題9>
渋谷教育学園幕張中学校 一次 2023年
次の各問いに答えなさい。
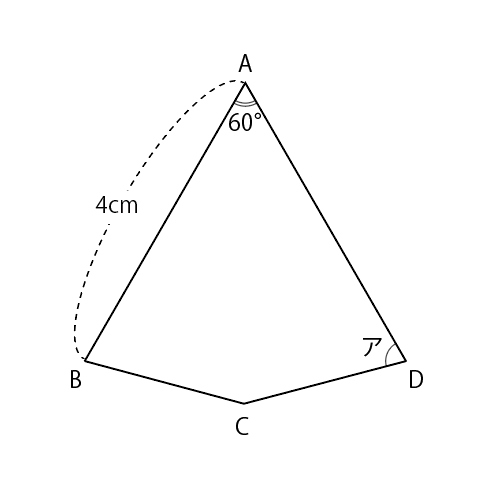
(1) 2つの合同な二等辺三角形をくっつけて、(図1)のような四角形ABCDをつくりました。AB=AD=4cm、BC=CDで、BCの長さはABの長さより短いとします。
① (図1)で、角アの大きさを求めなさい。
② (図1)で、四角形ABCDの面積を求めなさい。
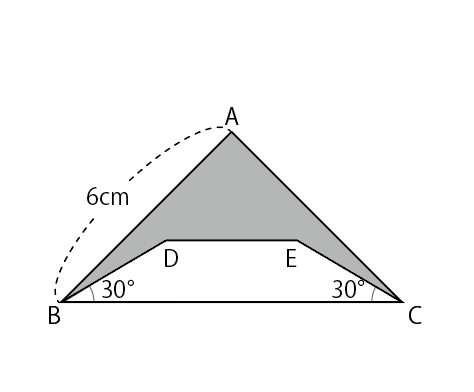
(2) (図2)で、三角形ABCはAB=AC=6cmの直角二等辺三角形、BD=DE=ECとします。(図2)の色をつけた部分の面積を求めなさい。
| (図1) | (図2) |
 |
 |
※中学校の許可を得て掲載しています。
【解答】
(1) ①75° ②8㎠
(2) 9㎠
【解説】
(1)
①
三角形ABCとADC は合同な二等辺三角形です. 角CAD = 60°/2 = 30°なので,
ア = 角CDA = (180 °– 30° )/2 = 75°です.
②
三角形ABCの三角形の面積は, ACを底辺としてみると高さは BからACに下ろした垂線の長さです. これは正三角形ABDの一辺の長さの半分で, 2cmです.よって三角形ABCの面積は
4 × 2 / 2 = 4㎠ で, 三角形ACD の面積も4㎠ なので, 答えは合わせて8㎠です.
(2)
前問のように、頂角が30°の二等辺三角形の面積は等辺が分かれば求めることができます. 頂角が30°の二等辺三角形を作るようにうまく補助線を引きたい気持ちになります.
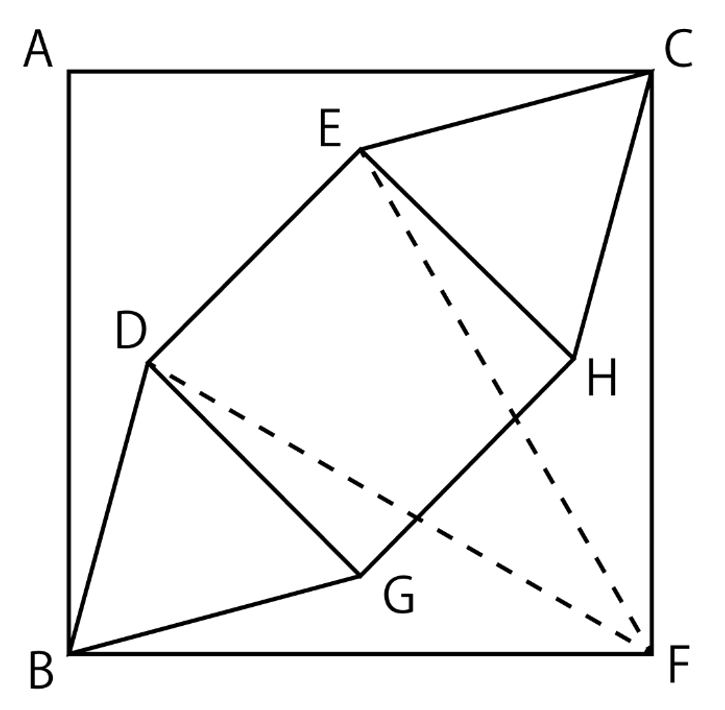
点A,D,Eを辺BCで折り返した点をF,G,Hとおきます. BD=BG, 角DBG=60°なので三角形BDGは正三角形で, 同様に三角形CEHは正三角形になります. 丁寧に図を書くと, 三角形ADE, FHGも正三角形であるように見え, 「三角形FDBとFEDとFCEが, 頂角が30°で等辺が6cmの二等辺三角形になる」(*)ことが予想できます. 実際にこれは正しく, 四角形ABDECは正方形ABFCから頂角が30°で等辺が6cmの二等辺三角形3つを除いた図形なので, 求める答えは6×6 – (6×3 / 2)×3 = 9㎠となります.
<(*)の証明>(難しいです.)
DG, EHとBCの交点をP, Qとします. DGとBC, EHとBCは垂直なので, DGとEHは平行です. DP=EQ, 角DPQ=角PQEより四角形DPQEは長方形で, 同様に四角形GPQHは長方形です. したがって四角形DGHEは長方形で, さらにDG=DB=DEより隣り合う辺の長さが等しいので, 四角形DGHEは正方形です.
正方形DGHEの対角線の交点をO, GHの中点をRとおきます. まずBOFは直角二等辺三角形なのでOB=OF, 次に四角形OPGRは正方形なのでOP=OR, そしてO,R,Fは同一直線上にあるので, BP = OB – OP = OF – OR = FR です. BP=FR, PG=RG, 角BPG = 角FRG より 三角形BPGと三角形FRGは合同です. したがって, 対応する辺の長さは等しいのでBG = GF です.
二等辺三角形BGFについて, 角BGF = 角 ABD = 45°-30°= 15°なので,
角BFG = 角FBG = 15°, 角BGF = 180°- 15°× 2 = 150°です.
よって角DGF = 360°-60°-150°=150°, BG = DG, GF = GF より三角形BGFとDGF は合同です. したがって, BF = FD で, かつ角BFD = 15°× 2 = 30°です.
三角形BFD が BF =FDをみたす頂角30°の二等辺三角形であることが分かりました. 同様に三角形EFC が EF =FCをみたす頂角30°の二等辺三角形であることが分かります.
これらよりDF=BF=CF=EF, 角DFE = 90°- 30°× 2 = 30°なので,
三角形DFEがDF = FEをみたす頂角30°の二等辺三角形であることが分かります. よって(*)は示されました.
(*)の証明が長いです. もっと簡単な方法があるかもしれません.