＜問題５＞
栄東中学校　東大特待Ⅰ(１教科)　2023年

　(1)図1の二等辺三角形を12個並べて、図2の図形をつくりました。図2の図形の面積は、1辺の長さが1cmの正三角形何個分ですか。

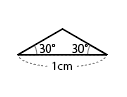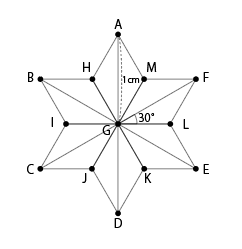図１ 図２

　(2)図2の点をそのまま使い、半径1cmの円と直線を加えて図3の図形をつくりました。
図3の影のついた部分の面積は、1辺の長さが1cmの正三角形何個分ですか。

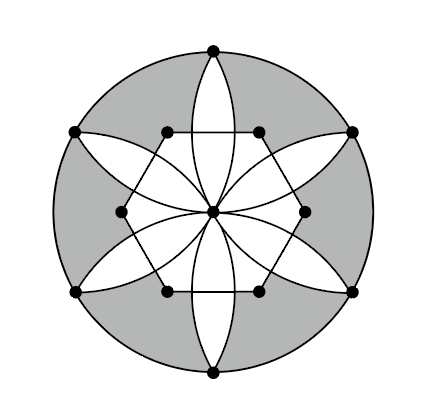
図３

※中学校の許可を得て掲載しています。

【解答】

(1)4個分
(2)4個分

【解説】

(1) 図１の二等辺三角形を3つ集めて, 等辺でくっつけると一辺1の正三角形ができます. 図2は図１の二等辺三角形が12コ集まってできているので, 一辺1の正三角形12/3 = 4個分です.
　
(2) 曲線が厄介ですね。そのまま面積を求めるのは算数では難しそうです. 上手い事等積変形できないでしょうか？

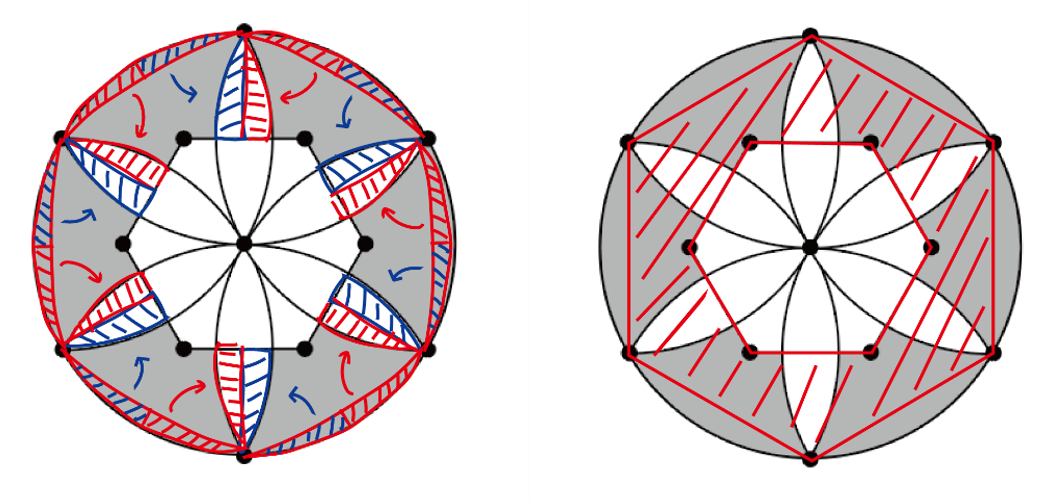
はい，できました. 大きい正六角形は図１の二等辺三角形が3×6=18コ集まって, 小さい正六角形は図１の二等辺三角形が6コ集まってできたものなので, 求める答えは
(18-6)/3 = 4コです.