
算数オリンピックも「いいね!」
2023年中学入試問題を紹介!

<問題4>
開智中学校 算数特待 2023年
ある燃料置き場から線路が引いてあり、線路には燃料置き場から一定の距離ごとに停留所があります。
汽車Aは燃料を4kg積むことができ、燃料1kgでとなりの停留所まで動くことができます。停留所では汽車に積んでいる燃料を下ろしたり、積んだりすることができます。ただし、最初はどの停留所にも燃料は置いてありません。
また、燃料置き場には大量の燃料が置いてあり、燃料がつきることはありません。
例えば、燃料を4kg積んだ状態で燃料を下ろさず動いていくと、4つはなれた停留所まで着きます。
しかし、1つはなれた停留所に燃料を1kg下ろすと、3つはなれた停留所までしか行けません。
さらに、1つはなれた停留所と2つはなれた停留所に燃料を1kgずつ下ろすと、2つはなれた停留所までしか行けません。
また、例えば1つはなれた停留所に燃料を1kg置いてきたあとに、燃料を4kg積んだ状態で燃料を下ろさず動いていくと、1つはなれた停留所の燃料を積むことができるので、5つはなれた停留所まで着きます。
(1) 燃料置き場から5つはなれた停留所に汽車が着くには、少なくとも何kgの燃料が必要ですか。ただし、5つはなれた停留所から燃料置き場までの帰りの燃料は数えません。
(2) 燃料置き場から6つはなれた停留所に汽車が着くには、少なくとも何kgの燃料が必要ですか。ただし、6つはなれた停留所から燃料置き場までの帰りの燃料は数えません。
いま、燃料を4kg積むことができ、燃料0.5kgでとなりの停留所まで動くことができる汽車Bが発明されました。
(3)燃料置き場から6つはなれた停留所と燃料置き場との往復を考えます。汽車Aで必要な燃料の重さ(kg)は、汽車Bで必要な燃料の重さ(kg)の何倍ですか。
【解答】
(1)7kg
(2)12kg
(3)8倍
【解説】
(1)
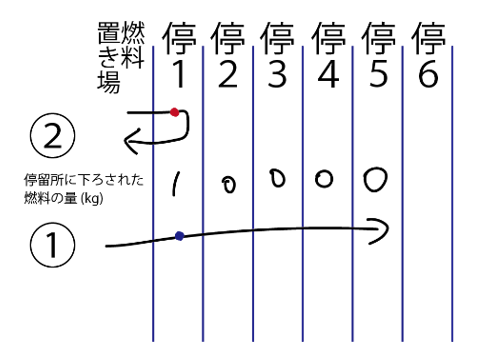
燃料置き場からn個離れた停留所を単に「停留所n」と呼ぶことにします.
燃料を4個積んだ状態で燃料置き場に戻らずに, 停留所5まで行くことは不可能です . そのため停留所に燃料をうまく下ろしてから, 燃料置き場から停留所5まで燃料を補給しながら行くことを考えます. まとめると, 以下の②→①の順に汽車を動かします.
①燃料置き場→停留所5
②(①を実行するために, ) 燃料置き場→停留所に積む→燃料置き場
①に必要な燃料は5kgで, 初めに4kg積めるので, 途中で燃料を1kg積む必要があります. ①にて途中で1kg積むために, ②では燃料置き場→停留所1に1kg下ろす→燃料置き場と列車を動かせばよいです. このとき必要な燃料は②で3kg, ①で4kgです.
よって答えは3 + 4 = 7 (kg) です.
図で赤い〇は1kg燃料を下ろしたこと, 青い〇は1kg燃料を積んだことを表します.
(2)
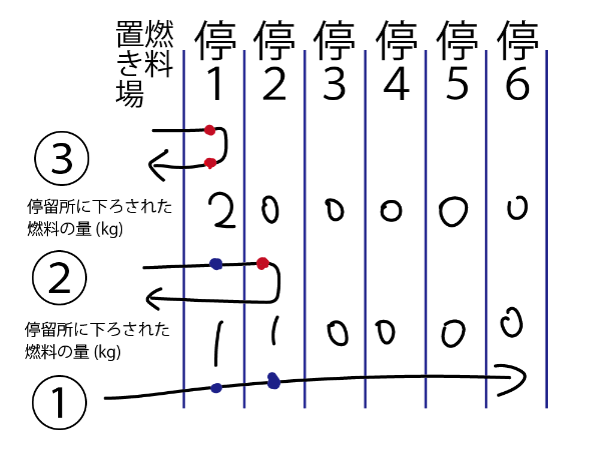
同様に, ①燃料置き場→停留所6を達成するには, 停留所1と2で1kgずつ燃料を積む必要があります.
①を達成するために②燃料置き場→停留所2→燃料置き場 と移動しますが, 停留所1で1kg燃料を積む必要があります. ①と②で合わせて合計2kgが停留所1にあればよいです.
②を達成するために③燃料置き場→停留所1→燃料置き場 と移動して, 停留所1で2kg燃料を下ろせばよいです.
したがって, 使う燃料は③で4kg, ②で4kg, ①で4kgなので, 4+4+4=12(kg)です.
(3)
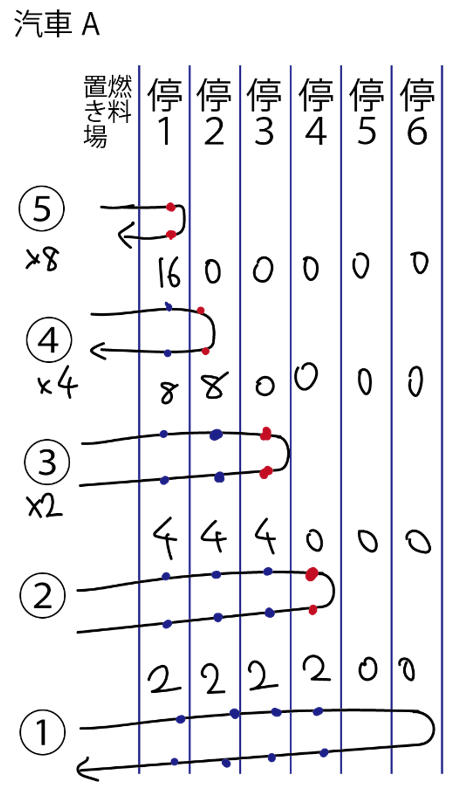
同様に①から順番に決めていくと, 汽車Aは⑤を8回, ④を4回, ③を2回, ②,①とすれば燃料置き場と停留所6を往復できます. このとき必要な燃料は4×(8+4+2+1+1)=64(kg)です.
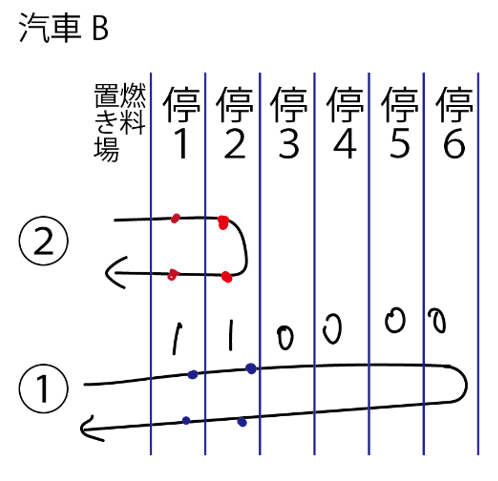
汽車Bは ②,①とすれば燃料置き場と停留所6を往復できます. このとき必要な燃料は4+4=8 (kg)です.
よって答えは, 64 ÷ 8 = 8 (倍)です.