＜問題２＞
淑徳与野中学校　第1回　2023年

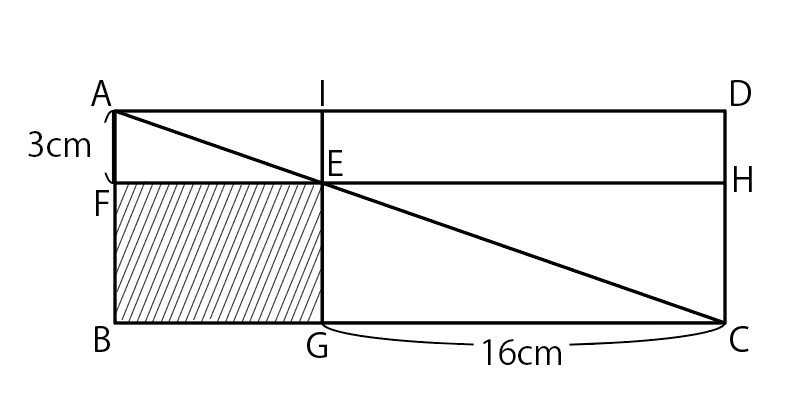
右の図で、四角形ABCDと四角形FBGEと四角形IEHDは長方形であり、点EはAC上の点です。
AFの長さが3cm、GCの長さが16cmのとき、斜線部分の面積は何cm2ですか。

【解答】

48

【解説】

図形は一意に定まりません. しかし面積は一意に定まります.

<解法1>相似を使う
三角形AFEとEGCは相似です. (平行線の錯角を用いて, 角FEA=角GCE, 角EAF=角CEGとなることから示せます. ) よってAF:FE = EG:GC なので, 3 : FE = EG : 16 です.
比の内項と外項の積は等しいのでFE×EG = 3×16 = 48 ですが, FE×EGはまさに長方形BFEGの面積を表しています. よって答えは48㎠です.

<解法2>パズルをする
三角形ABC, AFE, EGC はそれぞれ三角形CDA, EIA, CHEと合同で, 面積が等しいです.
長方形BFEGは三角形ABCから三角形AFEとEGCを除いたもので,
長方形DHEIは三角形CDAから三角形EIAとCHEを除いたものなので,
二つの長方形の面積は等しくなります. よって長方形DHEI の面積を求めればよく, 答えは 3×16 =48㎠です.