
算数オリンピックも「いいね!」
2023年中学入試問題を紹介!

<問題19>
筑波大学附属駒場中学校 2023年
次の図1または図2のマスに、0から9までの数を1つずつ書くことを考えます。
| 図1 | 図2 |
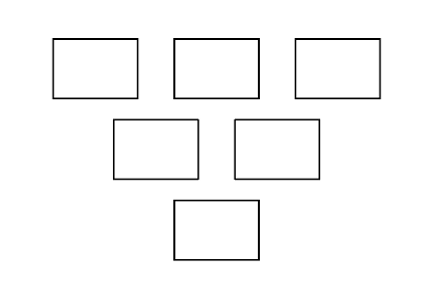 |
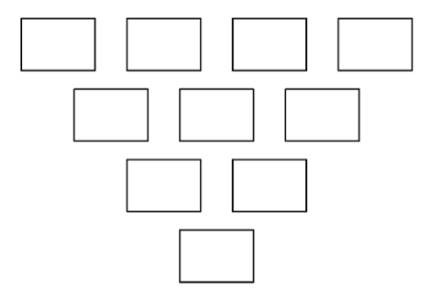 |
図のマスに数を書く<きまり>は次の通りです。
| <きまり> | ① | はじめに、3けたの整数、または4けたの整数を、1けたずつに分けて、図の一番上の段のマスに書きこむ。3けたのときは図1を、4けたのときは図2を使う。 |
| ② | 同じ段の、となりあう左右2つのマスに書かれた数のうち、大きい数から小さい数をひき、その結果を2つのマスのすぐ下のマスに書く。ただし、2つのマスの数が同じときは0を書く。 | |
| ③ | 図の一番下の段のマスに数が書かれるまで、②をくり返す。 |
例えば、次のように、はじめの整数が2023のとき、<きまり>にしたがって最後に書かれる数は1です。
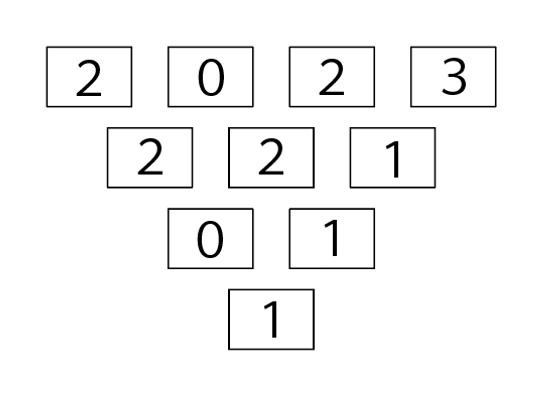
次の問いに答えなさい。
- 次の図は、<きまり>にしたがって数を書いた結果の一部です。はじめの3けたの整数として考えられるものをすべて答えなさい。
- 100から999までの900個の整数のうち、<きまり>にしたがって最後に書かれる数が9であるものをすべて答えなさい。
- 100から999までの900個の整数のうち、<きまり>にしたがって最後に書かれる数が8であるものは何個ありますか。
- 1000から9999までの9000個の整数のうち、<きまり>にしたがって最後に書かれる数が8であるものは何個ありますか。
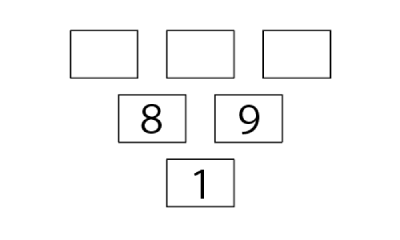
※中学校の許可を得て掲載しています。
【解答】
(1)190, 809
(2)900, 990
(3)9コ
(4)26コ
【解説】
極端なところから攻める!算数の鉄則です.
下から1段目 , 2段目, 3段目, 4段目と呼ぶことにします.
(3)以降では慎重な場合分けが必要です. 特に(3)で間違えると(4)に響いてくるので要注意です. 先頭が0であるか否かに注意しましょう.
(1)
差が9になる0から9までの数の組は(0,9), (9,0)のどちらかです. 十の位が0のとき百の位は8, 十の位が9のとき百の位は1, と決まるので, 答えは190, 809 です.
(2)
2段目で場合分けします.
二段目が[0] [9] :
3段目の数は一番右が0または9であることから考えて, [9][9][0], [0][0][9] のどちらかです. 問題の条件より3段目の一番左は0でないので, 考えられるのは[9][9][0]です.
二段目が[9][0] :
3段目の数は一番左が9であることから考えて, [9][0][0]のみが考えられます.
よって, 答えは 900, 990です.
(3)
(2)の解法より, 下の段に[9]がある段は, [9]から考えると簡単だと感じられます. これを踏まえて, (3)でも2段目を場合分けします.
| 1段目 | 2段目 | 3段目 |
| 8 | 08 | 008, 119, 880, 991 |
| 19 | 109, 890 | |
| 80 | 088, 199, 800, 911 | |
| 91 | 098, 901 |
百の位が0のものを除いて, 答えは9コです.
(4)
同様にやるだけです. 大変です.
ここでは表で書いていますが, 樹形図で書いた方が楽だと思います.
(樹形図で解説しようとしたらとても図が縦に伸びてしまったもので……)
あらかじめ4段目は、千の位が0になるものは除きます.
| 1段目 | 2段目 | 3段目 | 4段目 |
| 8 | 08 | 008 | 1119, 8880, 9991 |
| 119 | 2109, 7890, 9890 | ||
| 880 | 1911, 8088, 9199 | ||
| 991 | 9098 | ||
| 19 | 109 | 1009, 8990 | |
| 890 | 8099, 1900 | ||
| 80 | 088 | 1191, 8808, 9919 | |
| 199 | 1090, 8909 | ||
| 800 | 1999, 8000, 9111 | ||
| 911 | 9010, 9012 | ||
| 91 | 098 | 9908 | |
| 901 | 9001 |
答えは10+4+10+2=26コです.