
算数オリンピックも「いいね!」
2023年中学入試問題を紹介!

<問題18>
慶應義塾中等部 2023年
[図1]、[図2]のような筆算で表せる3桁の整数の計算を考えます。9つの数字1、2、3、4、5、6、7、8、9を図の○の位置に1つずつ置いて、正しい計算になるようにします。それぞれの図において、同じ数字は用いないものとして、次の に適当な数を入れなさい。
- [図1]の筆算で表せるような3桁の整数の和を考えます。その和は最も小さい場合で になります。
- [図2]の筆算で表せるような3桁の整数の差を考えます。その差は最も大きい場合で になります。
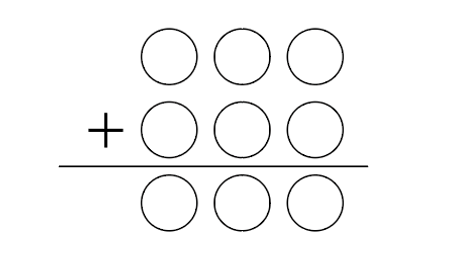
[図1]
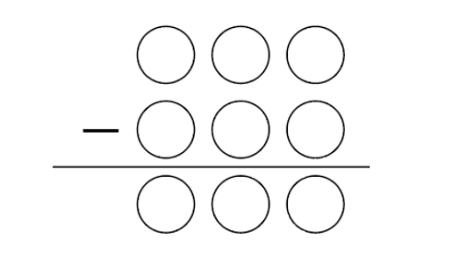
[図2]
※中学校の許可を得て掲載しています。
【解答】
(1)459
(2)784
【解説】
厳密にやると難しいです.
極端な場合から考えます.
(1)
和を小さくしたいので, まず足す2数の百の位を1と2にします. このとき, 和の百の位が3と仮定すると, 和は最小でも146+257 = 403 となり不適です. よって和の百の位は4です.
1○○+2〇〇=4〇〇 となり、余った数は3,5,6,7,8,9です.
足す1の位の2数は, (3+5=8), (3+6=9), (6+7=13), (7+8=15), (7+9=16), (8+9=17)の6種類考えられます. それぞれの組について十の位に余った数を適切にあてはめてば, (3+6=9)のときの173+286=459が, 和が最小になります. 求める答えは459です.
(2)
解説の便宜上,
ABC
―DEF
───
GHI
と〇に記号をつけます.
差の百の位をなるべく大きくしたいので, A=9, D=1 とします.
差の百の位が8のとき, 十の位で繰り下がりは起こりません. B,C,E,F,H,Iで使われる数字は2,3,4,5,6,7です. 一の位で繰り下がりが起こらないと仮定すると, B - E = H , C – F = Iとなります. しかし,
B + C + E + F + H + I = B + (E + H) + C + (F + I)
= 2 × (B + C)
= 2 + 3 + 4 + 5 + 6 + 7
=27
より2×(B+C)が奇数になるので不適です.
従って一の位で繰り下がりは起こり, このとき B – E – 1 = H , 10 + C – F = Iです.
B – E – 1 = H となる組(B, E, H) は (6, 2, 3)(6, 3, 2)(7, 2, 4)(7, 4, 2)
10 + C – F = I となる組(C, F, I) は (2, 5, 7)(2, 7, 5)(3, 6, 7)(3, 7, 6)
ですが, すべての数が異なる組(B, F, H, C, F, I)は存在しません. よってG =8は不適です.
次にA=9, D=1で, G=7のときを考えます. 十の位で繰り下がりが起こります. B,C,E,F,H,Iで使われる数字は2,3,4,5,6,8です. 一の位で繰り下がりが起こらないと仮定すると, 10 + B - E = H , C – F = Iとなります. このとき,
B + C + E + F + H + I = B + (E + H) + C + (F + I)
= 2 × (B + C) + 10
= 2 + 3 + 4 + 5 + 6 + 8
=28
より B+C = 9 です. このとき,
10 + B – E = H となる組(B, E, H) は (2, 4, 8)(2, 8, 4)(3, 5, 8)(3, 8, 5)(4, 6, 8)(4, 8, 6)
C – F = I となる組(C, F, I) は(5, 2, 3)(5, 3, 2)(6, 2, 4)(6, 4, 2)(8, 2, 6)(8, 3, 5)(8, 5, 3)(8, 6, 2)
です. このうちすべての数が異なる組(B, F, H, C, F, I)は, B + C = 9 に着目すると
(3, 5, 8, 6, 2, 4)(3, 5, 8, 6, 4, 2)(3, 8, 5, 6, 2, 4)(3, 8, 5, 6, 4, 2) の4組あります. このうち3桁の整数GHIが最も大きくなるような数は, 936 – 152 = 784 です.
一の位で繰り下がりが起こると仮定すると, B + C + E + F + H + I を計算すると偶奇に関する矛盾が起こるので不適です. よってA = 9, D = 1のときの最大の差の値は784です.
差の値が784を超える可能性があるA = 8, D = 1のとき, A = 9, D = 2 のときを調べる必要があります. どちらの場合も784以上の差にしようとすると, 十の位は繰り下がらないので B – E = 8 となり, B = 9, E = 1 が決定します. このときDとE, または AとB が等しい数字になっているので, 不適です.
よって求める答えは
936
―152
───
784
です.
B+C+E+F+H+Iを見るところがこの解法で難しいところですが, これをしなくとも頑張れば解けると思います.