＜問題16＞
女子学院中学校　2023年

次の　にあてはまる数を入れなさい。

　2023枚の折り紙をJ、Gの２人で分けるのに、同じ枚数ずつJ、G、G、J、J、G、G、J、J…の順に取っていき、最後にその枚数が取れなかった場合も順番通りの人が残りをすべて取ることにします。例えば、２０枚ずつだとJは1020枚、Gは1003枚で、３０枚ずつだとJは1003枚、Gは1020枚もらえます。

  1. ２３枚ずつ取ると、Jは　枚もらえます。
  2. あ枚ずつだとJは1023枚もらえます。ただしあは素数です。

※中学校の許可を得て掲載しています。

【解答】

(1)1011枚
(2)31

【解説】

(1)
{ J, G, G, J }で周期になることに気づきます. 23枚ずつ取ると, 1周期でJとGはどちらも23×2 = 46枚ずつとります.
2023 ÷ (46 × 2) = 21 … 91 なので｛J, G, G, J｝を21周期繰り返した後, 91枚の折り紙が余ります.
91 ÷ 23 = 3 …22より, 91枚の折り紙はJ, G, Gがこの順に23枚ずつ取ったあとJが残りの22枚を取ってなくなります. よって求める答えは
46(枚) × 21(周期) + 23(枚) + 22(枚) = 1011(枚)です.

(2)
1023という数字だけに着目してしまうと何の取っ掛かりもなく上手くいきません.
ここで, (1) に戻ります. Jが1011枚ということはGが1012枚なので, Gの方が1枚だけ多く差とかなり僅差です. これは確かに, あと折り紙が1枚多くあれば {J, G, G, J}の周期がちょうど終わりにJとGの枚数の差が0になるので, 1枚差になるのが納得いきます.
Jが1023枚とるということはGが1000枚取るということです. JがGより23枚多く折り紙を取るとはどういうことでしょうか？
JがGより多く折り紙を持っているとき、最後の折り紙を取ったのは, 周期{J G G J} の最初のJか, 最初のGです. 下図はJとGの折り紙の枚数の差のグラフです.


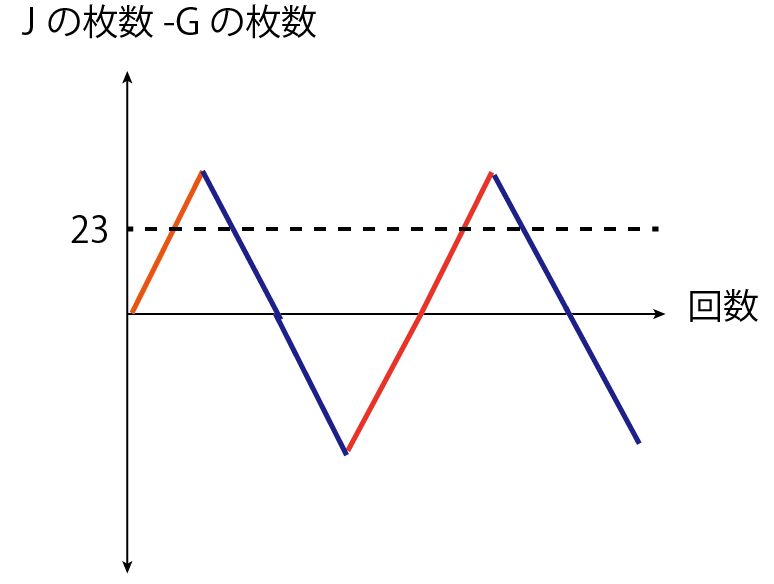
あ が23以上であることに気をつけて, 最後の折り紙を誰が取ったかで場合分けします.

[1] 周期{J,G,G,J}の最初のJで最後の折り紙を取った場合
もし折り紙があと23枚少なければ, JとGは合わせて2000枚折り紙を取って, 周期の繰り返しがちょうど終わっていました. 1周期で取られる折り紙の枚数は(4×あ)枚なので, 2000は(4×あ) の倍数です.
4×500 が 4×あ の倍数ということは, 500 は あ の倍数で, すなわち あ は500の約数です. しかし500の約数でかつ23より大きい素数は存在しないので, 不適です.

[2] 周期{J,G,G,J}の最初のGで最後の折り紙を取った場合
もし折り紙があと23枚あれば, 最後の人がもう23枚取り, JとGは合わせて2046枚折り紙を取って, 周期の途中{J, G}までがちょうど終わります. 1周期で取られる折り紙の枚数は(4×あ)枚なので, 2046は(4×あ)で割って(2×あ)余ります.
よって, 2046が(2×あ)の倍数ということは, 1023 は あ の倍数で, すなわち あ は1023の約数です. 1023 = 3×11×31の約数でかつ23より大きい素数は, 31のみです. 確かめてみると, 31は条件に適しています.
よって答えは31です.