＜問題14＞
広尾学園中学校　第1回　2023年

　円卓に何人かの人が座ります。座る人は【正直者】か【嘘つき者】のどちらかで、両隣の人について「はい」か「いいえ」で答える質問をしたとき、【正直者】は必ず正しいことを言い、【嘘つき者】は必ず正しくないことを言います。質問は円卓に座る全員にします。次の問いに答えなさい。

  • (1) 円卓に【正直者】が２人と【嘘つき者】が１人の合計３人が座っています。「両隣の人はどちらも【嘘つき者】ですか？」という質問に対して「はい」と答える人は何人いるか答えなさい。

  • (2) 円卓に【正直者】が３人と【嘘つき者】が２人の合計５人が座っています。次の(ア)～(エ)のうち正しいことを述べているものをすべて選び、記号で答えなさい。

    • （ア） 「両隣はどちらも【正直者】ですか？」という質問に対して、どの座り方であっても「はい」と答える人が少なくとも１人はいる。
    （イ） 「両隣はどちらも【嘘つき者】ですか？」という質問に対して、どの座り方であっても「はい」と答える人が少なくとも１人はいる。
    （ウ） 「両隣に【正直者】と【嘘つき者】が１人ずついますか？」という質問に対して、「はい」と答える人が４人となる座り方がある。
    （エ） 「両隣に【正直者】と【嘘つき者】が１人ずついますか？」という質問に対して、「はい」と答える人が１人となる座り方がある。

  • (3) 円卓に【正直者】が７人、【嘘つき者】が３人の合計１０人が座っています。「両隣に【正直者】と【嘘つき者】が１人ずついますか？」という質問に対して、「はい」と答える人は、最小で何人、最大で何人と考えることができますか。それぞれ答えなさい。

※中学校の許可を得て掲載しています。

【解答】

(1)1人
(2)イ, ウ
(3)最小で3人, 最大で9人

【解説】

正直者を〇、嘘つき者を×と表して図を書くと、考えやすくなります.
(3)ではとりあえず手を動かせば, 最大・最小になるために必要な性質が見つかると思います.

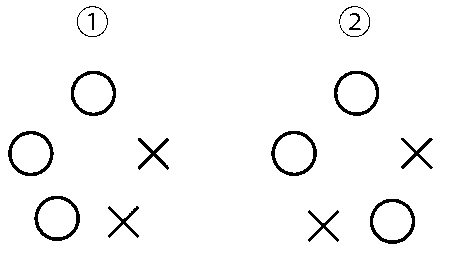
(1)
正直者2人と嘘つき1人を円卓の座り方は、回転・反転を区別しなければ左の1通りです. どの人も「両隣の人がどちらも嘘つき者」ではないので, 正直者2人は「いいえ」, 嘘つき者１人は「はい」と答えます. よって答えは1人です.

(2)
正直者3人と嘘つき2人を円卓の座り方は、回転・反転を区別しなければ上の2通りです. 2つの×の位置関係に注目すると正確に数え上げられます. ①,②の座り方に対して, ア～エの質問に「はい」と答える人が何人いるか調べ上げると(下表)、答えはイ、ウです.

(人) アの質問 イの質問 ウ・エの質問
① 3 2 2
② 0 3 4

(3)
最大・最小を求めるときは極端な場合から考えるのが手筋です.

【最大】
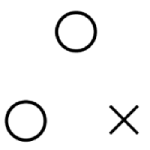
まず最大で何人かを求めます. 10人が可能かと考えて手を動かしてみると, どのように〇を7コと×を3コ書いても, 〇が3コ連続する箇所ができ, 3コ連続した〇の真ん中が「いいえ」と答えてしまいます. よって10人は不可能です. 〇が3コ連続する箇所を少なくするよう気を付けると, 9人は以下のように構成できます.

【最小】
最大を求めるときは〇が3コ連続する箇所を少なくするようにしました. つまり最小をもとめるときは〇をたくさん連続させればよいのではないでしょうか？この発想に基づくと3人は以下のように構成できます.
2人の構成が可能かを考えます. 〇が3コ以上連続するところで必ず両端の〇は「はい」と答えるので、その2人以外全員が「いいえ」と答えなくてはいけません. しかしその場合、いずれかの×が「はい」と答えてしまいます. よって, 不可能です.

したがって求める答えは最小で3人, 最大で9人 です.