＜問題13＞
普連土学園中学校　２日午後２科　2023年

　線をたどって２つの地点を移動するときの最短経路と最長経路を考えます。ただし、一度通った線は通れないものとします。
　例えば、図１で地点Pから地点Qまで移動することを考えると、図２のアは最短経路を、イは最長経路の１つを表しています。


　図１


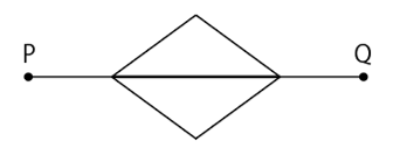
図２　（ア：最短経路） （イ：最長経路）

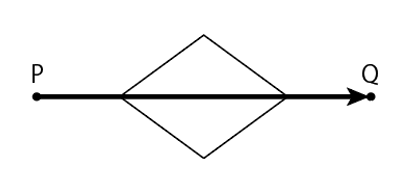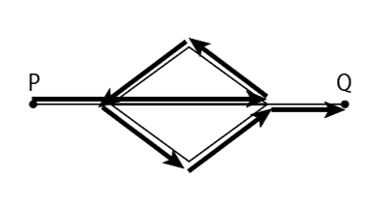図３で地点Aから地点Bまで移動します。このとき、次の問いに答えなさい。


図３

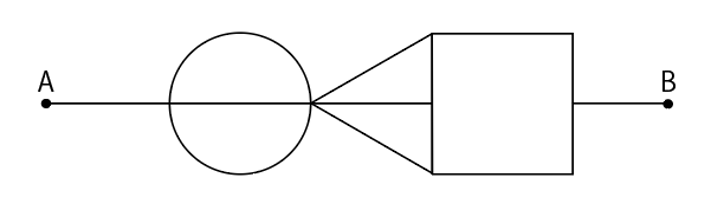
  1. 最短経路を解答欄の図に１通りだけかきなさい。また、全部で何通りあるか答えなさい。
  2. 最長経路を解答欄の図に１通りだけかきなさい。また、全部で何通りあるか答えなさい。

※中学校の許可を得て掲載しています。

【解答】

(1)例 (2)例

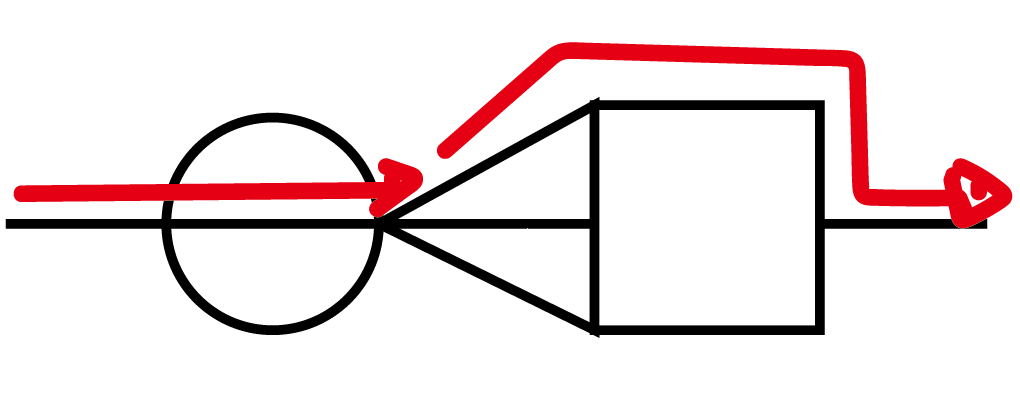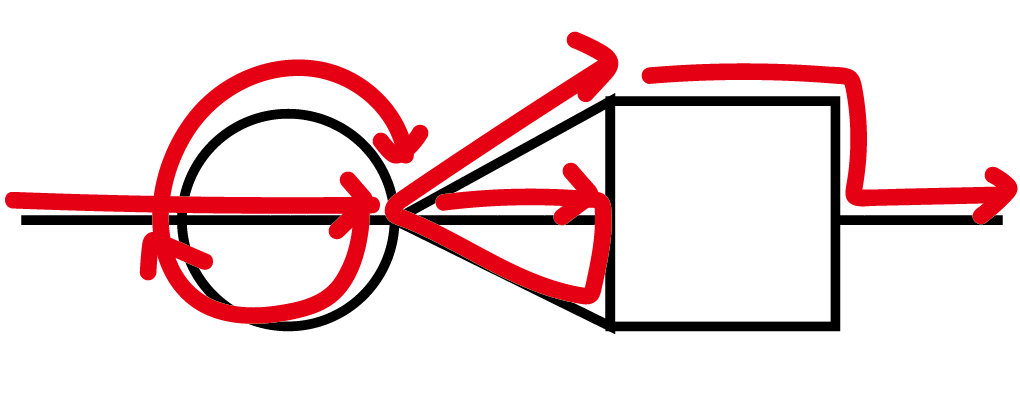(1)2通り
(2)48通り

【解説】

〇と◁の交点をCとします. 落ち着いて漏れなく考えましょう.

(1)
最短経路なので, 左から右に突き進む感覚で解いていきます.
経路はA→C→B の順番です.
A→C では, 真ん中の直線を進む方法が最短で, 1通りです.
C→Bでは, 上側か下側を進む方法の2通りです.
したがって答えは2通りです.

(2)
最長経路になりそうなものをいろいろ書いて試してみると、最長経路で通る線は図、または図の上下反転のどちらかになりそうだと予想できます. これは奇点・偶点に着目すれば実際に正しいことが分かります.
最長経路で通る経路が図になるような場合の数を求めます. (答えを求めるときに2倍します. )
はじめにA→Cを進む方法は3通りです.
Cからすぐに円に戻るとき, C → 円 → C は時計回りか反時計回りかで2通りあります. その後C → Bは直角三角形を通る向きで2通りなので, つまりこのとき C → B は2×2=4通りです.
C から三角形に行って、その後円に戻るとき, C → 三角形 → C は2通り, C → 円 → C は2通り, C → B は1通りで, つまりこのとき C → B は2×2=4通りです.
よって最長経路で通る経路が図になるような場合の数は, 3×(4+4)=24通りです.
図が上下反転する場合も考えて, 求める答えは48通りです.