
算数オリンピックも「いいね!」
2023年中学入試問題を紹介!

<問題10>
市川中学校 第1回 2023年
下の図のように、マス目に以下の手順で記号○、●を入れていきます。
・1番上の行のマス目にはすべて○を入れる。
・1番左の列のマス目にはすべて○を入れる。
・それ以外のマス目には、左のマス目と上のマス目に同じ記号が入っているときは●を、異なる記号が入っているときは○を入れる。
例えば、2行目2列目のマス目には、左のマス目にも上のマス目にも○が入っているため、●を入れます。
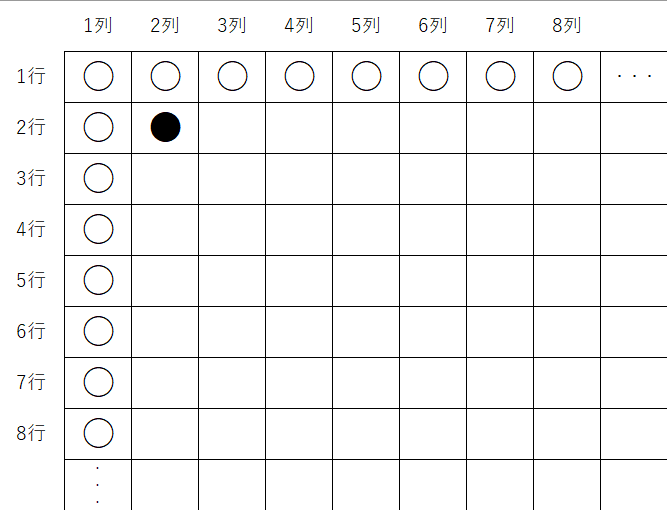
このとき、次の問いに答えなさい。
(1) 4行4列目までの16個のマス目には○と●がどのように入れられるか、【解答らん】の空らんの部分に○、●をかきなさい。
(2) 16行16列目までの256個のマス目に○と●を入れたとき、その中に含まれる○の個数を求めなさい。
(3) あ行目あ列目までのマス目に○と●を入れると、○の個数が1000個以上になります。あにあてはまる数の中で、最も小さいものを求めなさい。
※中学校の許可を得て掲載しています。
【解答】
(1)
| 1 | 2 | 3 | 4 | |
| 1 | 〇 | 〇 | 〇 | 〇 |
| 2 | 〇 | ● | 〇 | ● |
| 3 | 〇 | 〇 | ● | ● |
| 4 | 〇 | ● | ● | ● |
(2) 81
(3) 68
【解説】
実験→規則を見つける→応用, という問いの流れに乗りたいです.
(1)まずはやってみるしかありません.
(2)8行8列ぐらいを自力で埋めてみると, 法則に気づくはずです.
(3)あ の値がある数以上であることはすぐに分かりますが, あとは小さい順に試していくしかありません. 難問です.
| 1 | 2 | 3 | 4 | 6 | 7 | 8 | ||
| 1 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 |
| 2 | 〇 | ● | 〇 | ● | 〇 | ● | 〇 | ● |
| 3 | 〇 | 〇 | ● | ● | 〇 | 〇 | ● | ● |
| 4 | 〇 | ● | ● | ● | 〇 | ● | ● | ● |
| 5 | 〇 | 〇 | 〇 | 〇 | ● | ● | ● | ● |
| 6 | 〇 | ● | 〇 | ● | ● | ● | ● | ● |
| 7 | 〇 | 〇 | ● | ● | ● | ● | ● | ● |
| 8 | 〇 | ● | ● | ● | ● | ● | ● | ● |
(1)
左上の表の4行目4列目までの部分です. 〇の個数は9個です.
(2)
まず8行目8列目までを考えます. 上のようにマス目を4つに区切ります. このとき左上、右上、左下は(1)で考えた4行4列のマス目に入れられた記号と等しく、右下は全て●になります. したがって〇の個数は9×3=27個です.
つぎに16行目16列目までを考えます. 同様にマス目を4つに区切ります. このとき左上、右上、左下は先ほど考えた8行8列のマス目に入れられた記号と等しく、右下は全て●になります. したがって〇の個数は27×3=81個です.
(3)同様に32行32列目まで考えると〇の個数は81×3=243個,
64行64列目まで考えると〇の個数は243×3=729個,
128行128列目まで考えると〇の個数は729×3=2187個なので,
求める答えは64より大きく128以下です.
| 1~64 | 65 | 66 | 67 | 68 | |
| 1~64 | 729 | 64 | 32 | 32 | 16 |
| 65 | 64 | ● | ● | ● | ● |
| 66 | 32 | ● | ● | ● | ● |
| 67 | 32 | ● | ● | ● | ● |
| 68 | 16 | ● | ● | ● | ● |
上の表は68行68列目までを表しており, 整数はその範囲の〇の個数です.
65行目の1~64列目の〇の数は1行目の1~64列目の〇の数に等しいため, 64個あります.
66行目の1~64列目の〇の数は2行目の1~64列目の〇の数に等しく, 2行目は「〇●」を繰り返しているため, 32個あります. 67行目, 68行目も同様の作業を繰り返します.
65~68行65~68列の記号はすべて●です. このように68行68行目までの数字を埋めていくと, 以下が分かります.
65行65列目までの〇の個数は729 + 64 + 64 = 857個.
66行66列目までの〇の個数は857 + 32 + 32 = 921個.
67行67列目までの〇の個数は921 + 32 + 32 = 985個.
68行68列目までの〇の個数は985 + 16 + 16 = 1017個.
よって求める答えは68です.
パスカルの三角形に関する問題ですね. 「はじめ1番上の行と左の列にすべて1を書き込み, 左と上の数字を足したものを順々に書き込む」というルールの出題もよくみられます. 中学受験では規則性に結び付けられることが多い題材です.
2, 4, 8, 16…と区切っていったところで勘のいい方は察するかもしれませんが, この問題は2進数と深く関わりがあります.
【おまけクイズ】
2進数の演算を用いて, n行m列目の記号が〇か●か判定する, 簡単な方法を探してください. (小学生にはかなり難しい。高校生なら解けるはず)