＜問題8＞
麻布中学校　2024年

１から9999までの整数を小さい順につなげて書き並べ、数字の並びAを作ります。
数字の並びA　　　123456789101112・・・99989999
この数字の並びAを左から順に３つの数字ごとに区切り、整数の列Bを作ります。
整数の列B　　　123 , 456 , 789 , 101 , 112 , ・・・ , 999
ただし、３つの数字の一番左が０である場合には、左の０を取って２桁や１桁の整数にします。例えば、021は整数21、007は整数７になります。また、000は整数０にします。


以下の問いに答えなさい。

  1. Bの1001番目の整数を答えなさい。

  2. Aに数字０は何個現れるか答えなさい。

  3. Aの中で、20から30までを書き並べた部分に注目し、Bを作るときに区切られる位置に縦線を書きました。このとき、縦線のすぐ右にある数字０をすべて丸で囲むと、以下のようになります。


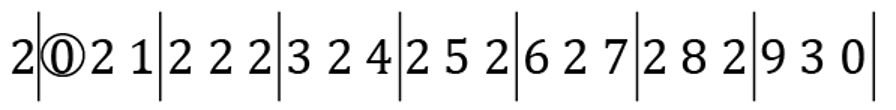
    4. これにならって、解答欄にある
    ● 1000から1003までを書き並べた部分
    ● 2000から2003までを書き並べた部分
    ● 3000から3003までを書き並べた部分
    に、それぞれBを作るときに区切られる位置に縦線を書き入れ、縦線のすぐ右にある数字０をすべて丸で囲みなさい。ただし、０が２個以上続いている場合も、縦線のすぐ右にある０だけを丸で囲みなさい。



  4. Bの中に100未満の整数は何回現れるか答えなさい。

※中学校の許可を得て掲載しています。

【解答】

（１）710　（２）2889個
（３）


（４）903個

【解説】

A、Bの中で、   １ケタの数を並べた部分を①、
         ２ケタの数を並べた部分を②、
         ３ケタの数を並べた部分を③、
         ４ケタの数を並べた部分を④とする。
このように場合分けをすると一気に分かりやすくなるはず。

  1. Aの中で、①～④の数がそれぞれいくつあるかを考える。
    ① １～９の９個の数があるので、１×９＝９
    ② 10 ～ 99の90個の数があるので、２×90＝180
    ③ 100 ～ 999の900個の数があるので、３×900＝2700
    ④ 1000 ～ 9999の9000個の数があるので、４×9000＝36000
     よって、①までの数は９個
         ②までの数は９＋180＝189個
         ③までの数は189＋2700＝2889個
         ④までの数は2889＋36000＝38889個
     Bの1001番目の数は、Aの3001～3003番目の数である。
     Aの3001番目の数は、3001－2889＝112より④の112番目の数。
     112÷４＝28だから、これは「1027」の７の部分にあたる。
     よって10271028の７から始まる３つの数が答えなので、答えは710。
  2. Aの中で一の位が０なのは…とやってもよいが、（４）があることを考慮して、①～④に場合分けする。
     ①：１ケタの数に０はないので０個
     ②：一の位に０があるのは９個、十の位には０はない。よって９個
     ③：一の位と十の位に０があるのは、10個に１個の割合なので、それぞれ90個
       百の位には０はない。よって90×２＝180個
     ④：一の位、十の位、百の位に０があるのは、10個に１個の割合なので、それぞれ
       900個
       千の位には０はない。よって900×３＝2700個
     したがって答えは９＋180＋900＝2889個。
  3. 「1000」の１は2890個目の数なので、2890÷３＝963・・・１。
    「2000」の２は2890＋４×1000＝6890個目の数なので、6890÷３＝2296・・・
    ２。
    「3000」の３は6890＋４×1000＝10890個目の数なので、10890÷３＝3630。
    よって答えは次のようになる。
  4. ①の部分で100未満の数は現れないので０回。
    ②の部分で０がBの百の位に来るものは、ちょうど３個に１個の割合なので３回
    （実際、20、50、80の０がBの百の位に来る）。
    ③の部分では、「100」の百の位の１は1890番目の数で、３でわって１あまるので、
    Bの百の位の数になる。よって100、101、102、103、…、999のように必ずもとの
    数の百の位がBの百の位の数になるので、０回。
    ④の部分を考える。（３）で○をつけた回数が、Bの数が100未満になる回数であ
    る。（３）より、「1000」から「3999」までの数を並べると下のようになる。

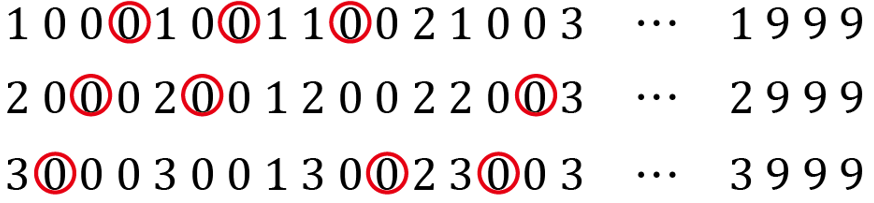
    これを見ると、０がある所では必ず縦に３個０が並んでいて、そのうちの１つに〇
    がついている。（証明は省略させていただきます）
    また「4000」から「6999」、「7000」から「9999」でも同様に、３個に１個の割合で〇がつく。
    よって（２）より④で一の位に０があるのは2700個なので、2700÷３＝900個。

    したがって答えは、０＋３＋０＋900＝903個。

＜コメント＞
（２）（３）が（４）のよい誘導になっていました。