＜問題7＞
麻布中学校　2024年

以下の問いに答えなさい。

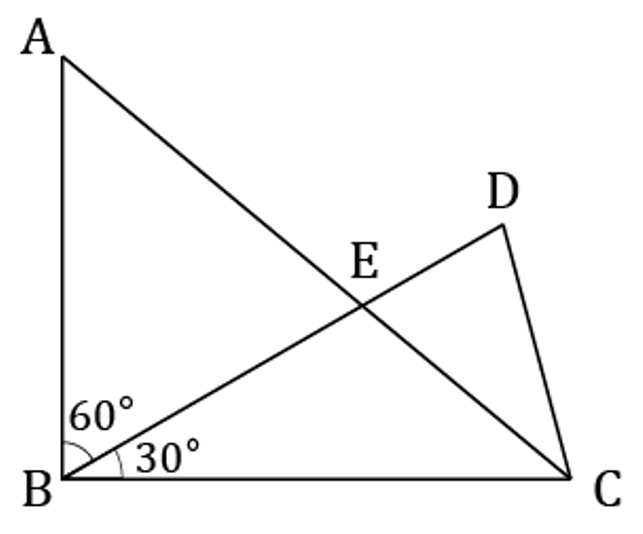
  1. 下の図において、AB=５cmであり、BC＝BD＝６cmです。三角形ABEの面積から三角形CDEの面積を引くと何cm2になりますか。
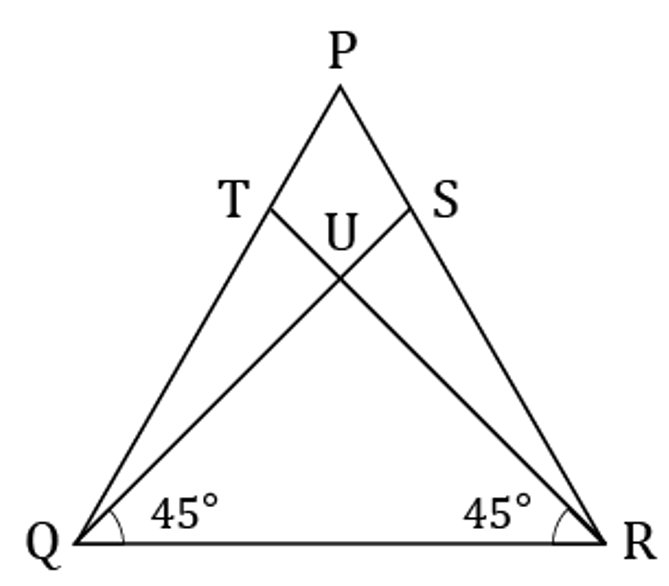
  2. 下の図において、QS＝５cmであり、三角形PQRは正三角形です。三角形UQRの面積から四角形PTUSの面積を引くと何cm2になりますか。

※中学校の許可を得て掲載しています。

【解答】

（１）６cm2　（２）6.25cm2

【解説】

  1. △ABEと△DECの面積はこのままでは比べにくいので、それぞれに△BECを足して考える。つまり、△ABEと△DECの面積の差は、△ABCと△DBCの面積の差と等しいことが分かる。
    △ABEは直角三角形なので面積は５×６÷２＝15cm2。
    △DBCは30°、75°、75°の三角形で斜辺が６cmだから面積は６×３÷２＝９cm2。
    よって△ABEと△DECの面積の差は15－９＝６cm2。
  2. （１）と同様に、△UQRと四角形PTUSのそれぞれに△TUQを足して考える。つまり、△UQRと四角形PTUSの面積の差は、△TQRと△PSQの面積の差と等しい。
    また、△TQRと△SRQは合同だから、△SRQと△PSQの面積の差を求めればよいと分かる。
    △PQRは正三角形だから、図のように△PQSと△RQS’が合同になるような点S’をとることができる。
    すると、求める面積は△SRQと△RQS’の差、つまり△SQS’の面積である。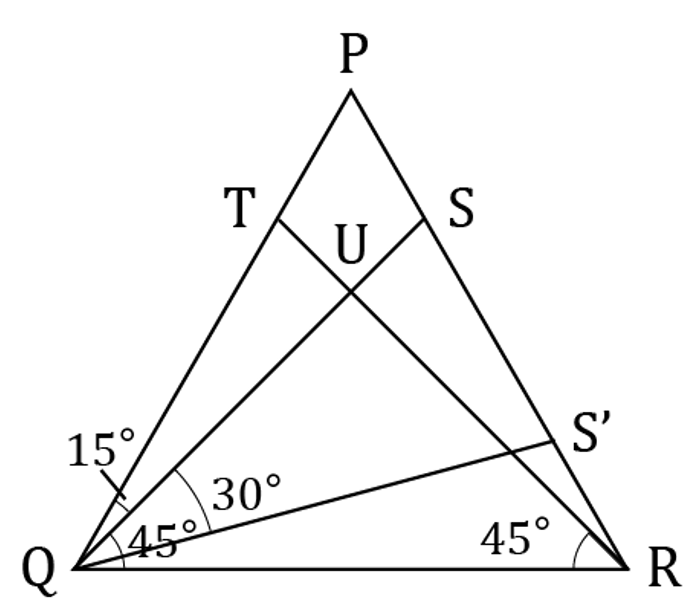
    ∠PQS＝∠PQR－∠SQR＝15°
    ∠S’QR＝∠PQS＝15°
    ∠SQS’＝∠PQR－∠PQS－∠S’QR＝30°となる。
    またSQ＝S’Qなので、三角形SQS’は30°、75°、75°の二等辺三角形だと分かる。
    SQ＝５cmなので、面積は５×2.5÷２＝6.25cm2。

＜コメント＞
（２）で補助線を考えるときに、「（１）が誘導になっているはずだから、30°75°75°の三角形を作ってみよう」、という感じで線を引いてみたら結果的にうまくいった、というのもアリかもしれないです。