＜問題５＞
渋谷教育学園幕張中学校　一次　2024年

次の各問いに答えなさい。
ただし、角すいの体積は、（底面積）×（高さ）÷３で求められるものとします。

（１）【図１】のように、立方体の展開図に点線をひきます。もとの折り目に加え、点線部分も折り目とし、すべての折り目が立体の辺になるようにして、この展開図を組み立てると、【図２】のような立体ができました。この立体の体積は何cm3ですか。

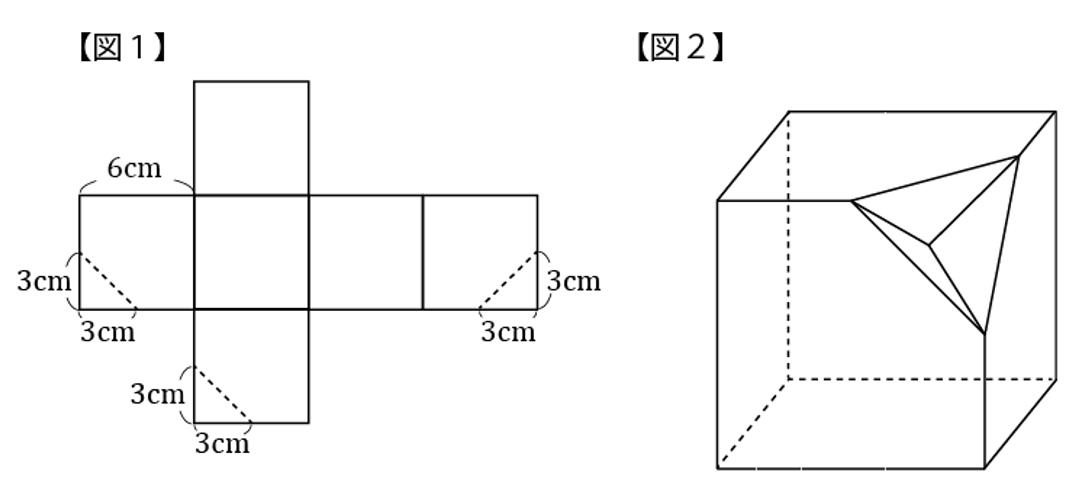
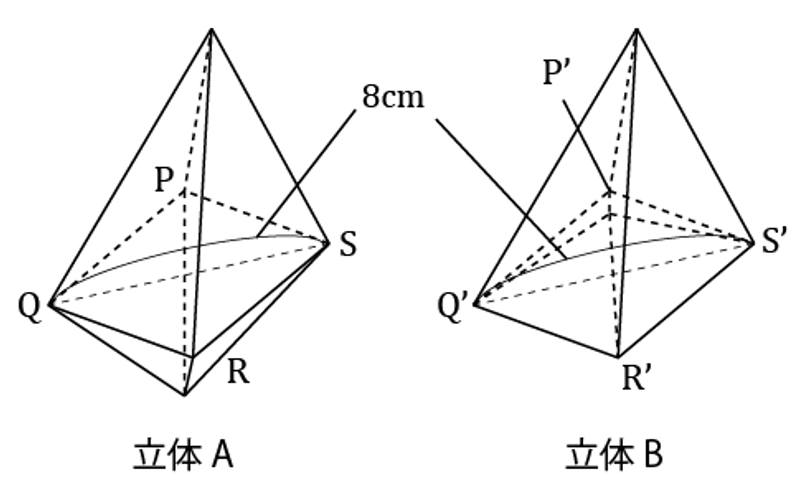
（２）【図３】のように、正方形BECDの対角線を一辺とする正三角形ABCを考えます。【図４】の展開図において、あ～えは合同な二等辺三角形で、お～くは【図３】の正三角形ABCと合同です。この展開図を組み立てて立体を作ると、二種類の立体が作れます。そのうち、体積が大きい方の立体を立体A、体積が小さい方の立体を立体Bとします。立体Aの体積は、立体Bの体積より何cm3大きいですか。

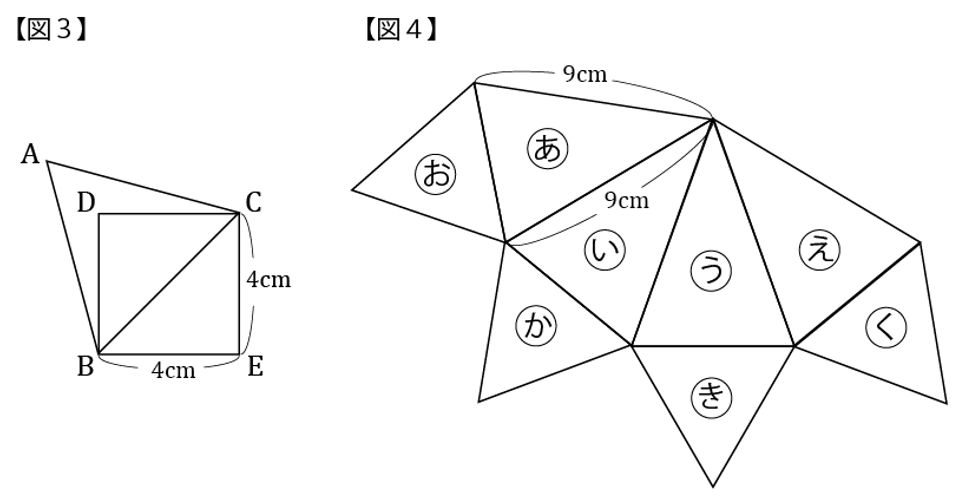
（３）【図５】の展開図において、ア～エは合同な台形で、オ～クは合同な正三角形です。この展開図を組み立てて立体を作ると、二種類の立体が作れます。そのうち、体積が大きい方の立体を立体C、体積が小さい方の立体を立体Dとします。２つの立体C、Dの体積の比（立体Cの体積）：（立体Dの体積）を、最も簡単な整数の比で答えなさい。

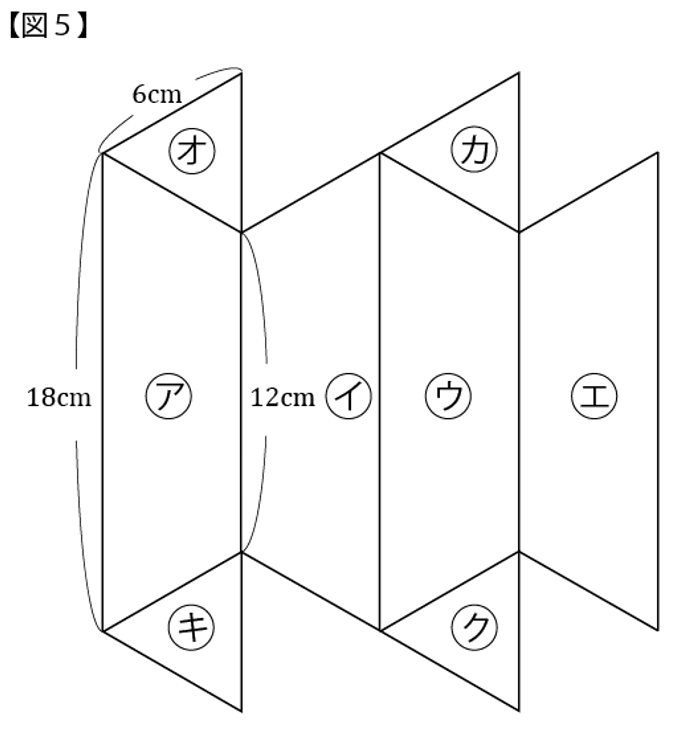
※中学校の許可を得て掲載しています。

【解答】

（１）207cm3　（２）85 1 ─ 3 cm3　（３）8：7

【解説】

  1. この立体は、下の図の立体Eから立体F（たて３cm、横３cm、高さ３cmの三角錐）をひいたものである。
    立体Eは、一辺が６cmの立方体から、立体Fをひいたものであるから、体積は
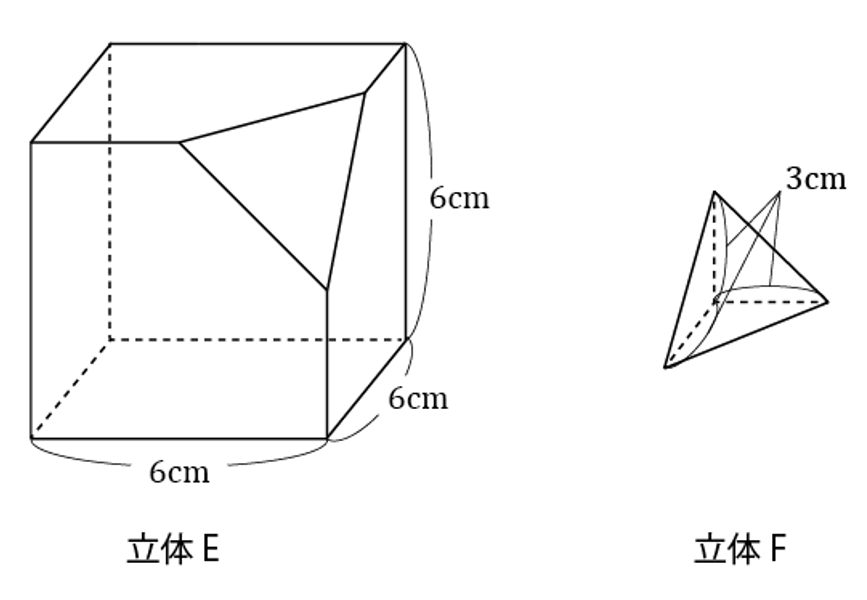
    ６×６×６－３×３× 1 ─ 2 ×３× 1 ─ 3 ＝ 216 － 4.5 ＝ 211.5cm3。 よって答えは211.5 － 4.5 ＝ 207 cm3。
  2. 立体Aはお、か、き、くの部分が出っぱっていて、立体Bはお、か、き、くの部分がへこんでいる。
    立体Aの四角形PQRS、立体Bの四角形P’Q’R’S’はともに正方形で、一辺の長さは正三角形お、か、き、くの一辺の長さと等しいので、対角線は８cmとなる。
    立体Aと立体Bの体積の差は、下の図の正八面体Gの体積と等しい。
    立体Gの赤色の正方形は、対角線の長さが８cmなので、面積は８×８× 1 ─ 2 ＝ 32cm3。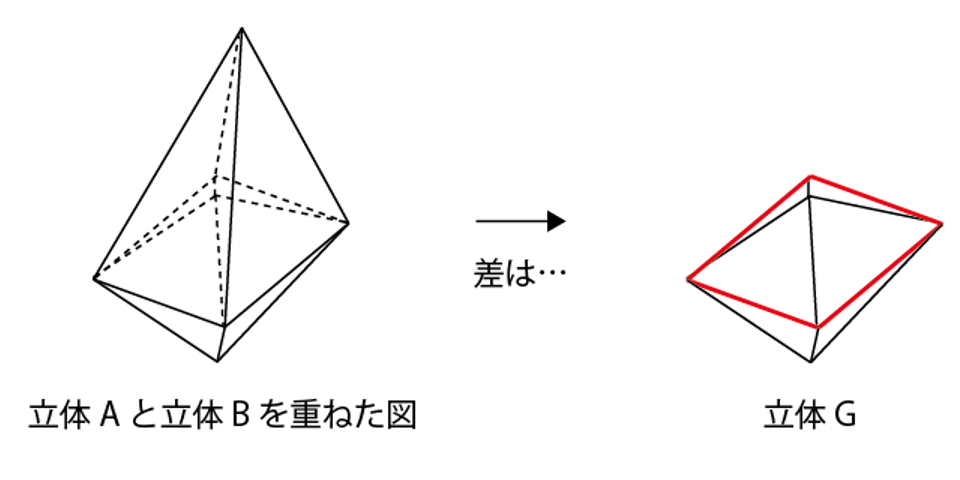
    よって立体Gの体積は32×8× 1 ─ 3 ＝ 256 ── 3 ＝85 1 ─ 3 cm3。
  3. 下の図の辺aがどこの辺と合わさるかを考えると、辺bと合わさる場合と、辺cと合わさる場合があることが分かる。
    辺aが辺bと合わさるとき：
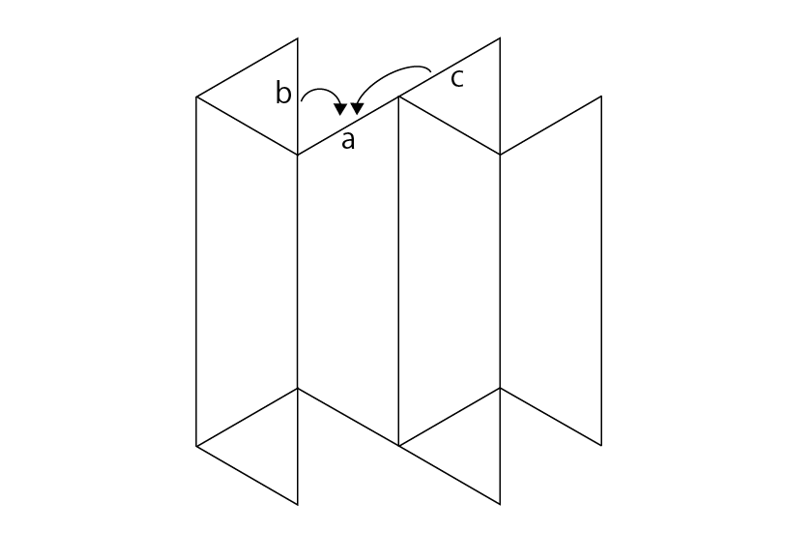
    ア、イ、オ、キを使ってできた立体を２つつなげた形になる。この立体を立体Hとする。
    辺aが辺cと合わさるとき：
    イ、ウ、カ、クを使ってできた立体を２つつなげた形になる。この立体を立体Hとする。
    上の図を見ると、立体Iよりも立体Hのほうが大きいことが分かるので、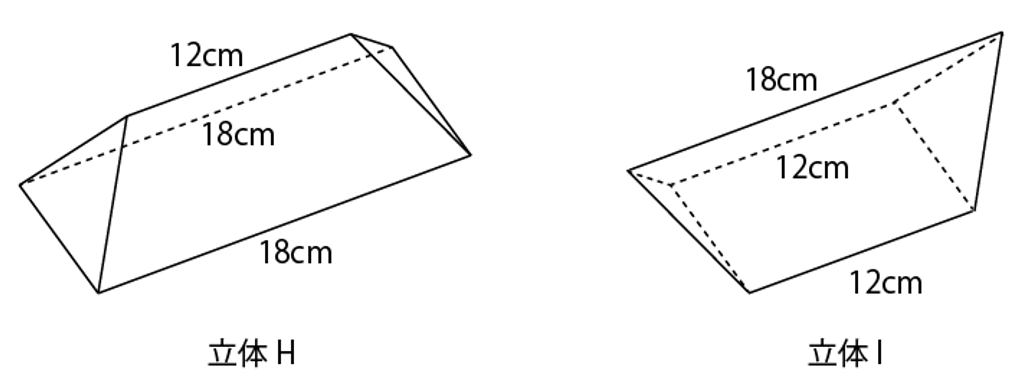
    立体H×２＝立体C、立体I×２＝立体Dである。
    よって体積の比は立体C：立体D＝立体H：立体I。
    立体Hと立体Iは、それぞれ断頭三角柱とみると、断面積が等しいので、立体Hと立体Iの体積の比はそれぞれの高さの比と等しいことが分かる。

    よって答えは 12+18+18 ──── 3 ： 12+12+18 ──── 3 ＝８：７。

＜コメント＞
立体H、立体Iを見たら、すぐに「断頭三角柱だ！」と分かるようにしておきましょう。