＜問題14＞
東海中学校　2024年

図のAB、AC、CDの長さはすべて同じで、BCとADの長さの差が５cmのとき、BEの長さを求めなさい。

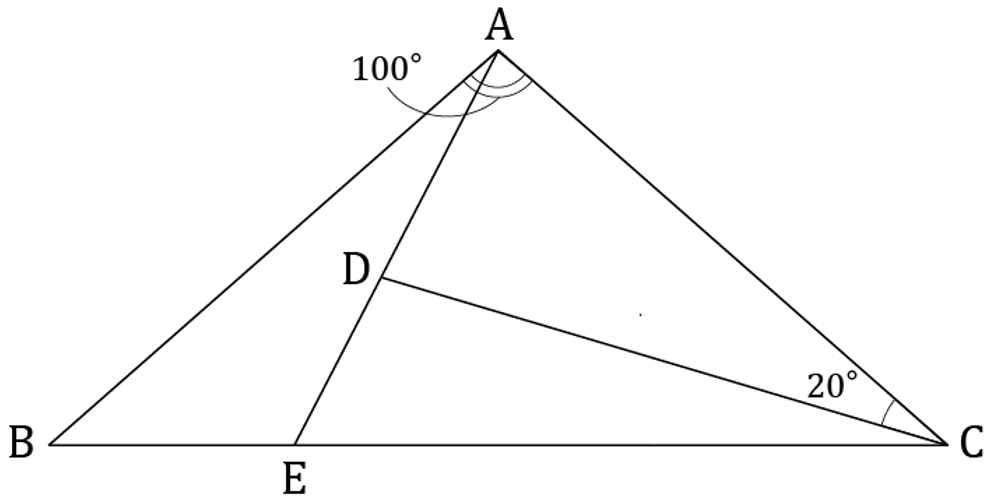
※中学校の許可を得て掲載しています。

【解答】

５ ─ ３ cm

【解説】

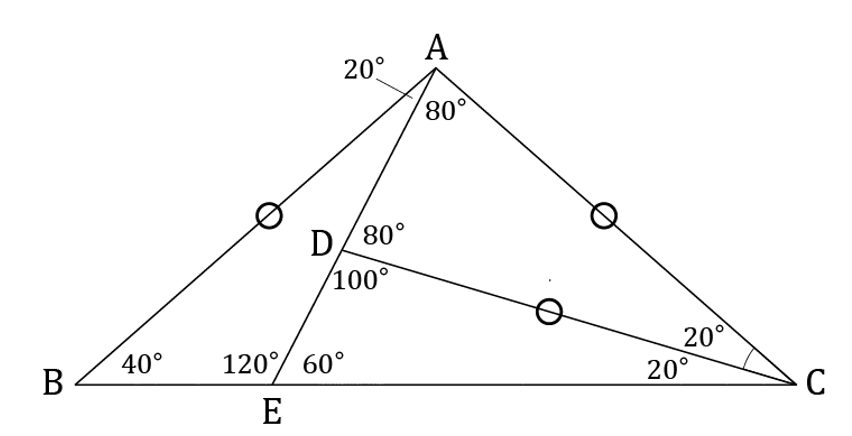
まずは分かる角度を図に書き入れていく。
△ADCは二等辺三角形なので、∠CAD＝∠CDA＝（180－20）÷２＝80°。
∠BACは100°なので、∠BAE＝100－80＝20°。
△BACは二等辺三角形なので、∠ABC＝∠ACB＝（180－100）÷２＝40°。
∠DCE＝∠ACE－∠ACD＝40－20＝20°。
∠AEB＝180－（20＋40）＝120°。
∠AEC＝180－120＝60°。
∠EDC＝180－80＝100°。

次に、AB=ACだから、△ABE≡△CAFとなるような点Fを、次の図のようにとる。

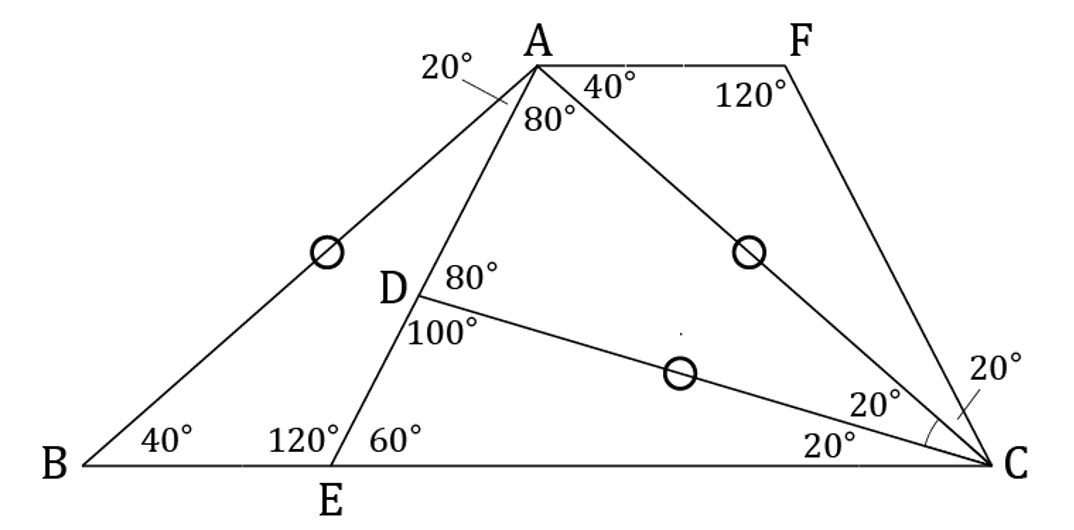
∠FAC＝40°＝∠ECAで、錯角が等しいことからAFとECは平行　…　①
また∠AEC＝60°、∠FCE＝20×３＝60°…　②
①②より、四角形AECFは等脚台形であり、ECを一辺とする正三角形ECGを次の図のように作ることができる。

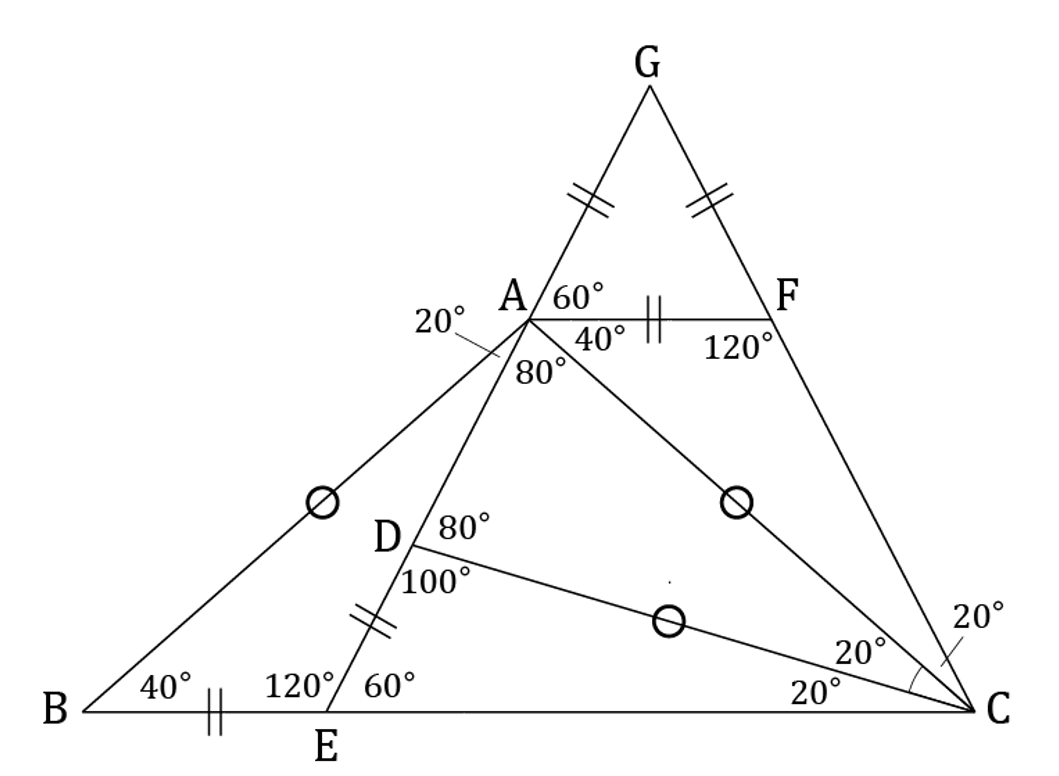
△GAFも正三角形になるから、GA=AF=FG。△ABE≡△CAFだから、AF＝BEと分かる。
また、AC＝DC、∠GAC＝∠EDC＝100°、∠ACG＝∠DCE＝20°なので、△GAC≡△EDCも分かる。よってGA=ED。
したがって、GA＝AF=FG=EB=ED、GE=EC=CG。
よって ５cm ＝BC－AD
        ＝BE＋EC－AD
        ＝BE＋GE－AD
        ＝BE＋ED＋AG
        ＝３×BE
答えはBE = ５ ─ ３ cm。