＜問題10＞
女子学院中学校　2024年

次の.にあてはまる数を求めなさい。
大きさの異なる２種類の正方形と円を図のように組み合わせました。小さい正方形１つの面積は８cm2、大きい正方形１つの面積は25cm2です。
斜線部分の八角形の面積は.cm2です。

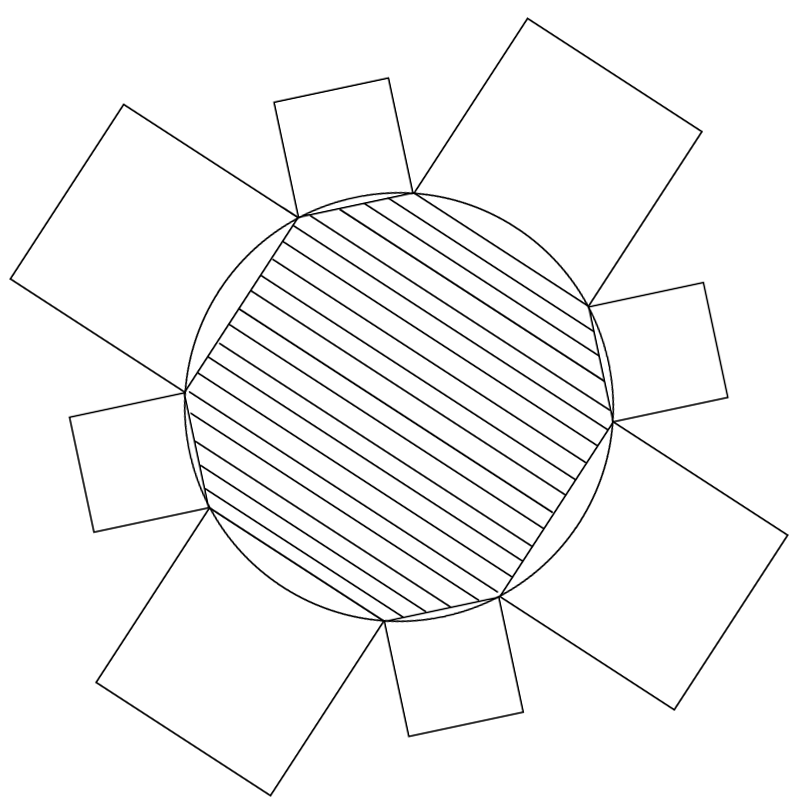
※中学校の許可を得て掲載しています。

【解答】

73cm2

【解説】

小さい正方形の面積は８cm2だから、対角線の長さは４cm。
また大きい正方形の面積は25cm2なので、一辺の長さは５cm。
下の図のように補助線を引くと、○印が２つ分で４cmなので、○印１つ分は２cm。
したがって図の○印をつけたところはすべて２cmである。
また、図の×印をつけたところはすべて５cmである。

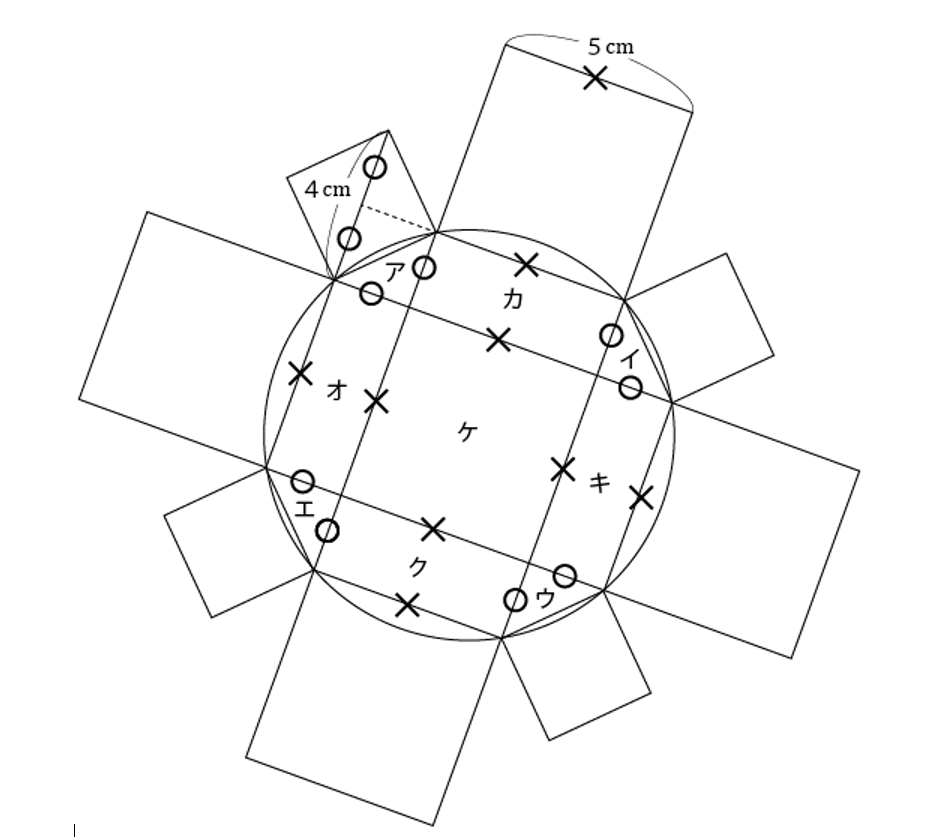
図のように細かく分けた部分をア～ケとおくと、
ア～エはそれぞれ２×２÷２＝２cm2。
オ～クはそれぞれ２×５＝10cm2。
ケは５×５＝25cm2。
よって求める面積は２×４＋10×４＋25＝73cm2。

＜コメント＞
大きな正方形をつくってからカドの直角二等辺三角形を４つひくのでもOKです。とにかく補助線をうまく引けるかがポイントです。