＜問題１＞
西大和学園中学校（東京・東海会場）　2024年

次の.にあてはまる数を求めなさい。
平行四辺形ABCDの内側に、直線BC上にない点Pを下の図のようにとります。
点Pを通り、直線ABと平行な直線と、辺BC、辺DAとの交点をそれぞれE、Fとします。（あ）の角の大きさは あ°であり、（い）の角の大きさはい°です。

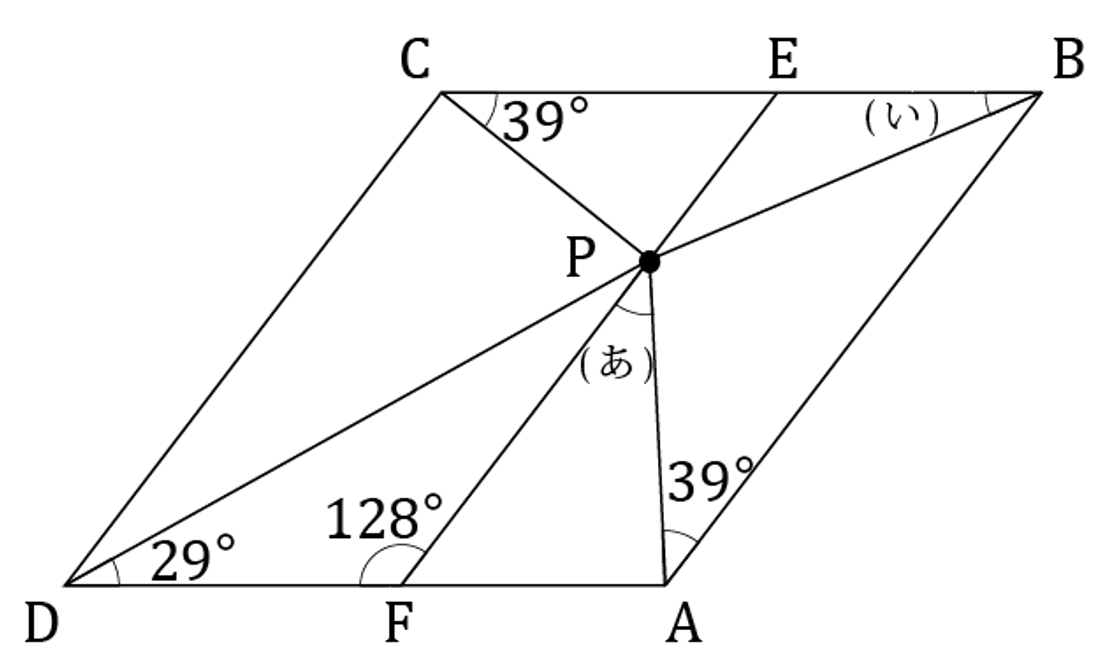
※中学校の許可を得て掲載しています。

【解答】

あ　39°　い　23°

【解説】

あ：
EFとBAは平行で、平行線の錯角は等しいから、∠PAB＝∠APF。
よってあ＝39°。

い：
図から分かる角度を書き込むと、下の図のようになる。

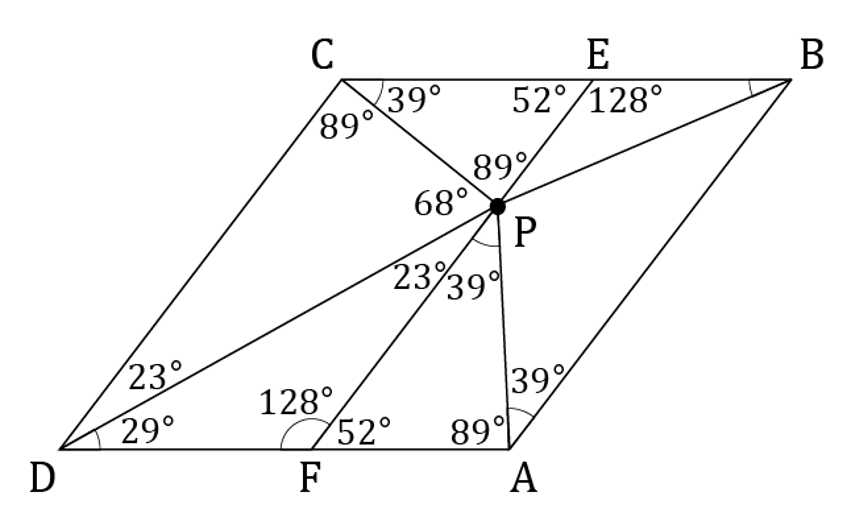
図より、△CPEと△PAFは相似。

下の図のように、CD上にQ、BA上にRをとり、直線QRがPを通り、CBと平行になるようにする。

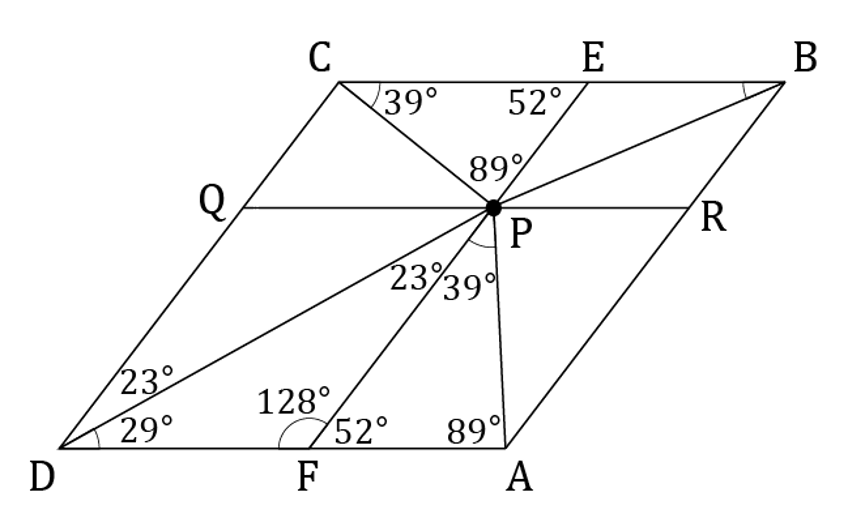
△CPEと△PAFは相似なので、EC：FP＝EP：FA。
EC＝PQ、FA＝PRなので、PQ：FP＝EP：PR。
したがって、平行四辺形QDFPと平行四辺形PRBEは相似。（ただし向きは違うので注意！）
よって、△PEDと△BEPは相似なので、い＝∠FPD＝23°。

＜コメント＞
相似の図形をうまく使いましょう。