＜問題８＞
広尾学園　2021年第1回

下の図のように，長方形ABCDの対角線AC上に点Eを，直線DE上に点Fをとります。直線BFが対角線ACと交わる点をGとします。三角形AEDの面積は63cm2，三角形ABGの面積は105cm2，三角形EGFの面積は12cm2です。次の問いに答えなさい。

(1) 直線BEを引きます。三角形ABEと面積の等しい三角形を1つ答えなさい。
(2) AE：EGを最も簡単な整数の比で求めなさい。
(3) 三角形FBDの面積を求めなさい。

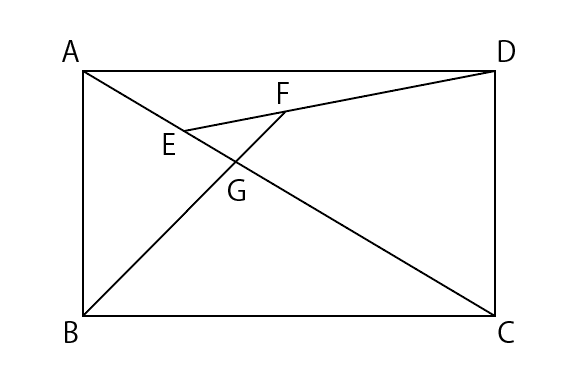
※中学校の許可を得て掲載しています。

＜解答＞

(1) 三角形AED
(2) 3：2
(3) 135cm2

＜解説＞

三角形EGDなどの大きい三角形の面積よりも，三角形FGDなどの小さい三角形の面積の方が図に書きやすいです。だから，なるべく小さい三角形の面積を図に書くとよいです。たとえば，大きい三角形EGDの面積が求まったら，それからすでに面積が分かっている三角形EGFの面積を引いて小さい三角形FGDの面積を求め，三角形FGDの面積を図に書くとよいです。
今回，解説の図には分かりやすさを優先したため書いていませんが，問題を解くときには分かった直線の長さの比や面積は全部図に書くとよいです。

(1) 辺ABの上にEHがABと垂直になるようにHをとり，辺ADの上にEIがADと垂直になるようにIをとります。すると，長方形AHEIと長方形ABCDは相似なので，HE：IE＝BC：DCです。だから，HE×DC＝IE×BC…①です。また，四角形ABCDは長方形なので，AB＝DC…②，AD＝BC…③です。


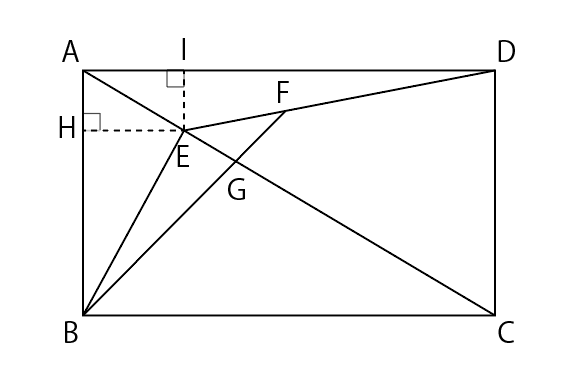
①と②と③から，
（三角形ABEの面積）
＝AB×HE÷2
＝DC×HE÷2
＝IE×BC÷2
＝IE×AD÷2
＝（三角形AEDの面積）
です。だから，答えは三角形AEDです。

(2) (1)から，三角形ABEの面積は三角形AEDの面積と同じで63cm2です。また，三角形ABGの面積は105cm2です。だから，三角形EBGの面積は三角形ABGの面積から三角形ABEの面積を引いて，105－63＝42(cm2)です。
よって，AE：EG
＝（三角形ABEの面積）：（三角形EBGの面積）
＝63：42
＝3：2です。
(3) AE：EG＝3：2と三角形AEDの面積が63cm2であることから，三角形EGDの面積は63× 2 3 ＝42(cm2)です。また，三角形EGFの面積は12cm2です。だから，三角形FGDの面積は三角形EGDの面積から三角形EGFの面積を引いて，42－12＝30(cm2)です。
よって，EF：FD
＝（三角形EGFの面積）：（三角形FGDの面積）
＝12：30
＝2：5　…④です。

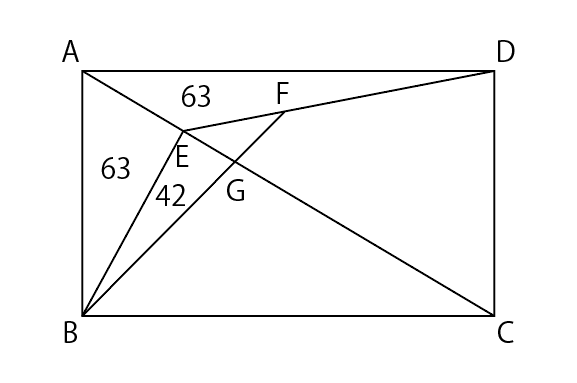
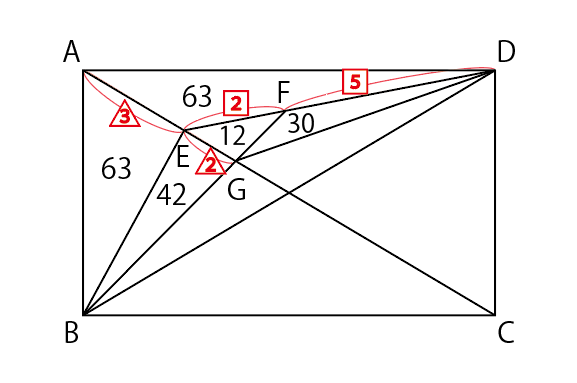
また，三角形FEBの面積は三角形EGFの面積と三角形EGBの面積を足して12＋42＝54(cm2)です。
このことと④から，三角形FBDの面積は54× 5 2 =135(cm2)です。