
算数オリンピックも感心!中学入試問題を紹介!
~メダリストはこう解く~

<問題7>
広尾学園 2021年第2回
燃料タンクの大きさも含めて同じ性能の自動車が同じ地点を出発し,同じ道を移動します。これらの自動車は,タンクいっぱいにガソリンを入れると,最大で600kmの距離を移動することができます。また,途中で他の自動車にガソリンの一部または全部をタンクいっぱいまで移すことができます。ただし,ガソリンが空になった自動車は,それ以上移動することができません。これらの自動車が複数台で同時に出発して,ガソリンを移すことでそのうちの1台ができるだけ長い距離を移動する方法を考えます。例えば,A,Bという2台の自動車で出発し,300km進んだところでAの残りのガソリンをすべてBに移すことで,Bは最大で900kmの距離を移動することができます。次の問いに答えなさい。
(1) A,B,Cの3台で出発をしてから,300km走ったところでAの残りのガソリンをすべてCに移しました。このあと,Cの走る距離をできる限り長くするために,どこかの地点でBの残りのガソリンもすべてCに移すことにします。そのようにして走ったとき,Cは出発してから何kmの距離を移動することができるか求めなさい。
(2) 3台の自動車が同時に出発して,そのうちの1台ができるだけ長い距離を移動するようにします。その1台は,最大で何kmの距離を移動することができるか求めなさい。
(3) 少なくとも1台が1400kmの距離を移動するには,最低何台の自動車で出発する必要があるか求めなさい。
※中学校の許可を得て掲載しています。
<解答>
(1) 1050km
(2) 1100km
(3) 6台
<解説>
(1) 300km移動してAの残りのガソリンを全部Cに移したとき,Bには300kmぶんの,Cには600kmぶんのガソリンがあるので,BとCは合わせて900km移動できます。B,Cが移動できる距離の合計が決まっているので,Cの移動する距離をなるべく長くするためには,Bの移動する距離はなるべく短くしないといけません。だから,Bの残りのガソリンを全部Cに移せるようになったらすぐに全部移さないといけません。
はじめに300km移動したあと,さらに①km移動したときに,Bの残りのガソリンを全部Cに移すとします。このとき,Bには(300-①)kmぶんの,Cには(600-①)kmぶんのガソリンが残っています。ここまでの状況を図にすると図1のようになります。
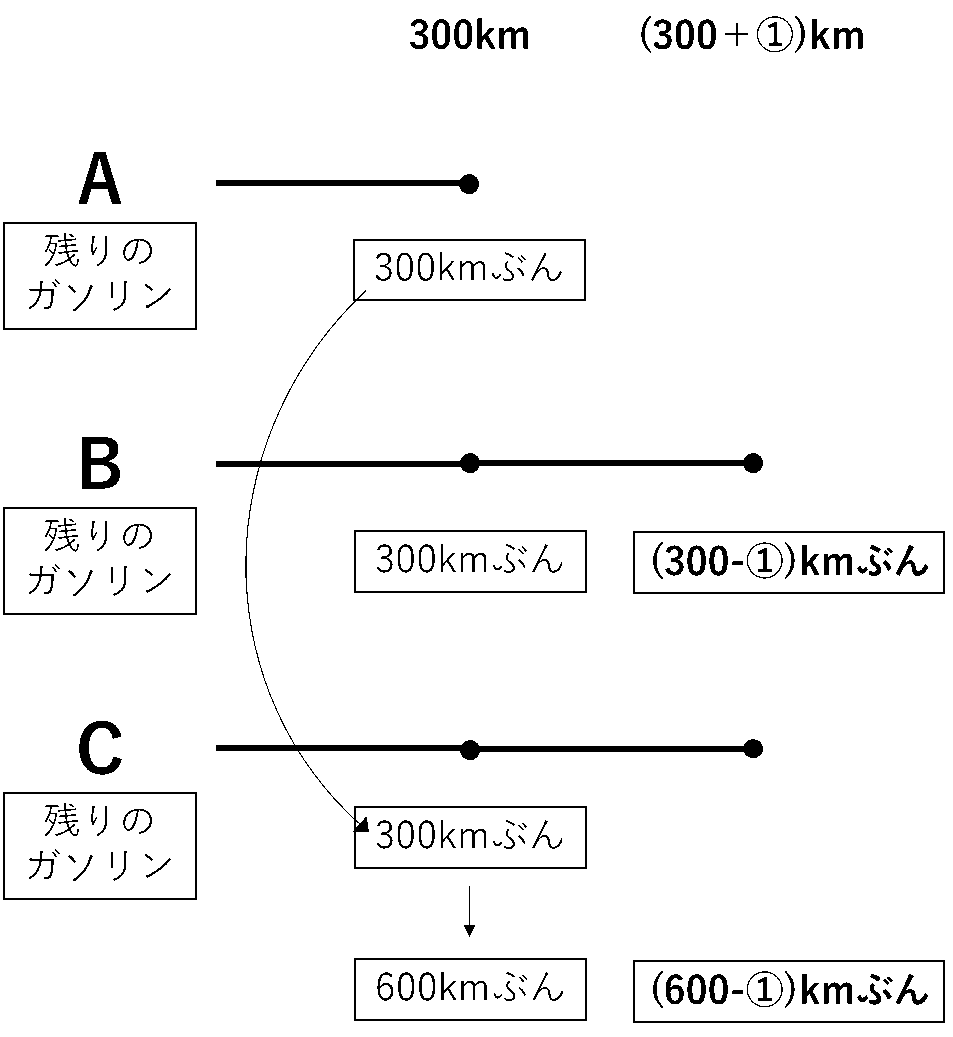 図1
図1
このとき,Cの燃料タンクは満タンになるはずで,そのためにはあと①kmぶんのガソリンを入れないといけませんので,これがBの残りのガソリンと同じ量になります。だから,300-①=①です。これを解くと,①=150です。
よってCは300km移動してから150km移動したあと,さらに600km移動できるので,Cは出発してから300+150+600=1050(km)移動できます。
(2) 3台の自動車にD,E,Fと名前をつけ,Eの移動する距離はDの移動する距離以上で,Fの移動する距離はEの移動する距離以上だとします。また,スタート地点をP,Dがそれ以上移動できなくなった場所をQ,Eがそれ以上移動できなくなった場所をR, Fがそれ以上移動できなくなった場所をS,とします。
はじめガソリンはD,E,F合わせて1800kmぶんあるので,D,E,Fの移動できる距離の和は1800kmです。また,Dがそれ以上移動できなくなったときにEとFに残っているガソリンの量の和は600+600=1200(km)ぶん以下です。だから,Dがそれ以上移動できなくなったあとEが移動できる距離とFが移動できる距離の和,つまりQRとQSの和は1200km以下です。さらに,Eがそれ以上移動できなくなったときにFに残っているガソリンの量は600kmぶん以下です。だから,Eがそれ以上移動できなくなったあとFが移動できる距離,つまりRSは600km以下です。
これまでの状況を下の図2のように書くと,
・黒の線の距離の和が1800km
・赤の線の距離の和が1200km以下
・青の線の距離が600km以下
となります。このとき,Fが移動する距離,つまりPSが最大で何kmかを求めます。
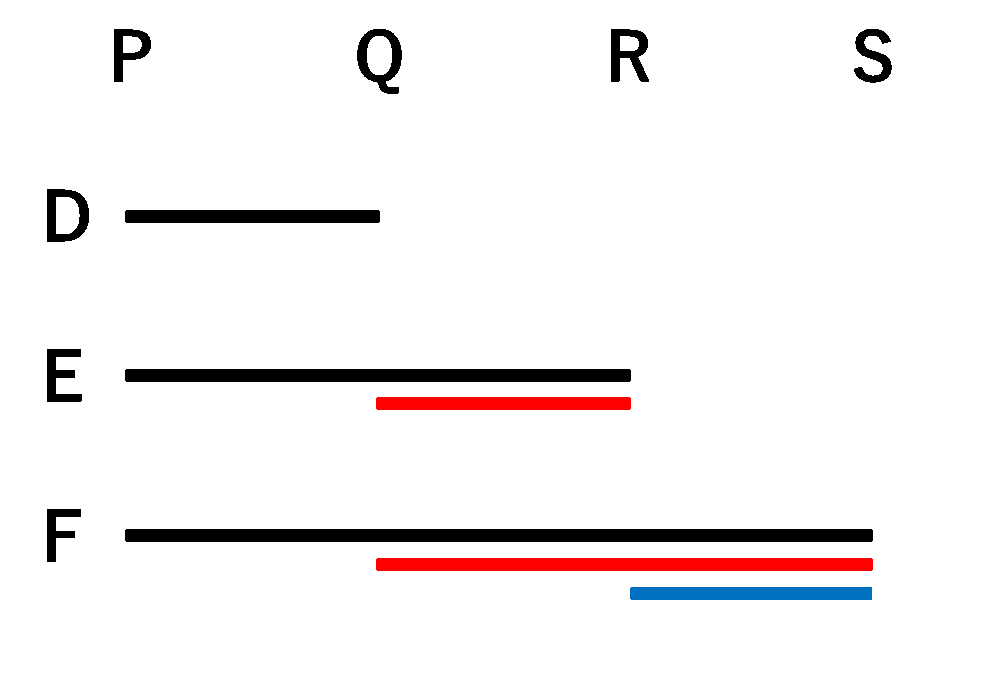 図2
図2
赤と青の線に注目します。下の図3のように,赤の線の距離と青の線の距離を足すと,QSの2倍になります。また,赤の線の距離の和が1200km以下,青の線の距離が600km以下なので,赤の線の距離と青の線の距離を足すと1800km以下です。つまりQSの2倍は1800km以下なので,QSは900km以下です。
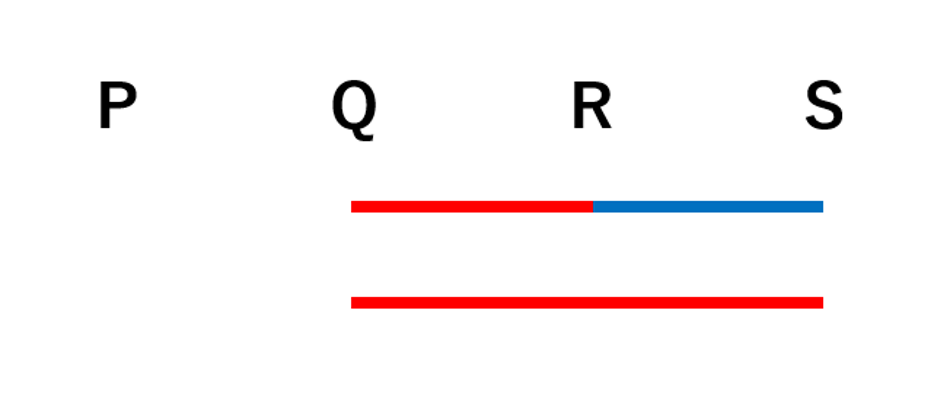 図3
図3
黒と青の線に注目します。下の図4のように,黒の線の距離と青の線の距離とQSを足すと,PSの3倍になります。また,黒の線の距離の和が1800km,青の線の距離が600km以下,QSが900km以下なので,黒の線の距離と青の線の距離とQSを足すと3300km以下です。つまりPSの3倍は3300km以下なので,PSは1100km以下です。
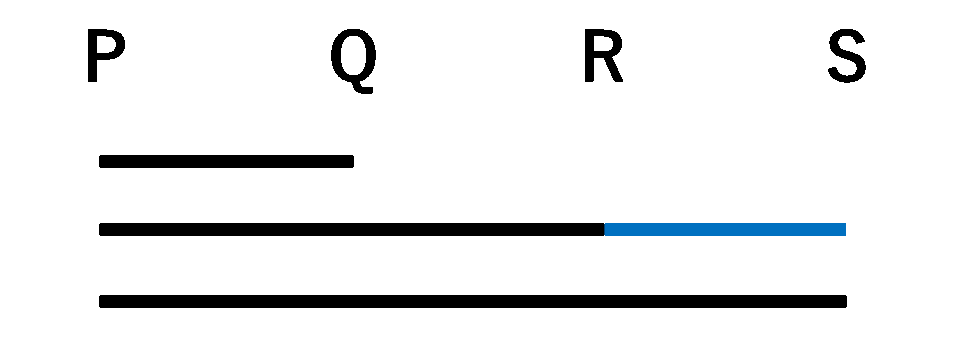 図4
図4
実際にPSが1100kmになることがあるのか考えます。PSの3倍は3300kmなので,黒の線の距離と青の線の距離とQSの和は3300kmです。このことと黒の線の距離の和が1800km,青の線の距離が600km以下,QSが900km以下であることから,青の線の距離はちょうど600km,QSはちょうど900kmです。だから,QSの2倍は1800kmとなり,赤の線の距離と青の線の距離を足すと1800kmです。このことと赤の線の距離の和が1200km以下,青の線の距離が600kmであることから,赤の線の距離の和はちょうど1200kmです。
図2に注目します。青の線の距離が600km なので,RSは600kmです。また,赤の線の距離から青の線の距離を引くとQRの2倍です。つまり,1200-600=600(km)がQRの2倍なので,QRは300kmです。さらに,黒の線の距離から赤の線の距離を引くとPQの3倍です。つまり,1800-1200=600(km)がPQの3倍なので,PQは200kmです。
まとめると,200km移動したところでDの残りのガソリンをEとFに半分ずつ移し,さらに300km移動したところでEの残りのガソリンを全部Fに移し,Fがさらに600km移動すると,Fは200+300+600=1100(km)移動できます。このとき,PSは実際に1100kmです。
よって答えは1100kmです。
☆論理的ではないが理解しやすい解説☆
3台の自動車にD,E,Fと名前をつけ,Eの移動する距離はDの移動する距離以上で,Fの移動する距離はEの移動する距離以上だとします。このとき,ガソリンは全部で600×3=1800(km)ぶんあるので,D,E,Fの移動できる距離の和は1800kmです。D,E,Fが移動する距離の合計が決まっているので,Fの移動する距離をなるべく長くするためには,Dの移動する距離やEの移動する距離はなるべく短くしないといけません。だから,Dの残りのガソリンを全部EとFに移せるようになったらすぐに全部移さないといけませんし,Eの残りのガソリンを全部Fに移せるようになったらすぐに全部移さないといけません。
DとEとFが1km移動したときにガソリンを移すとします。このとき,D,E,Fにはそれぞれ(600-1)kmぶんのガソリンが残っています。ここまでの状況を図にすると下の図5のようになります。
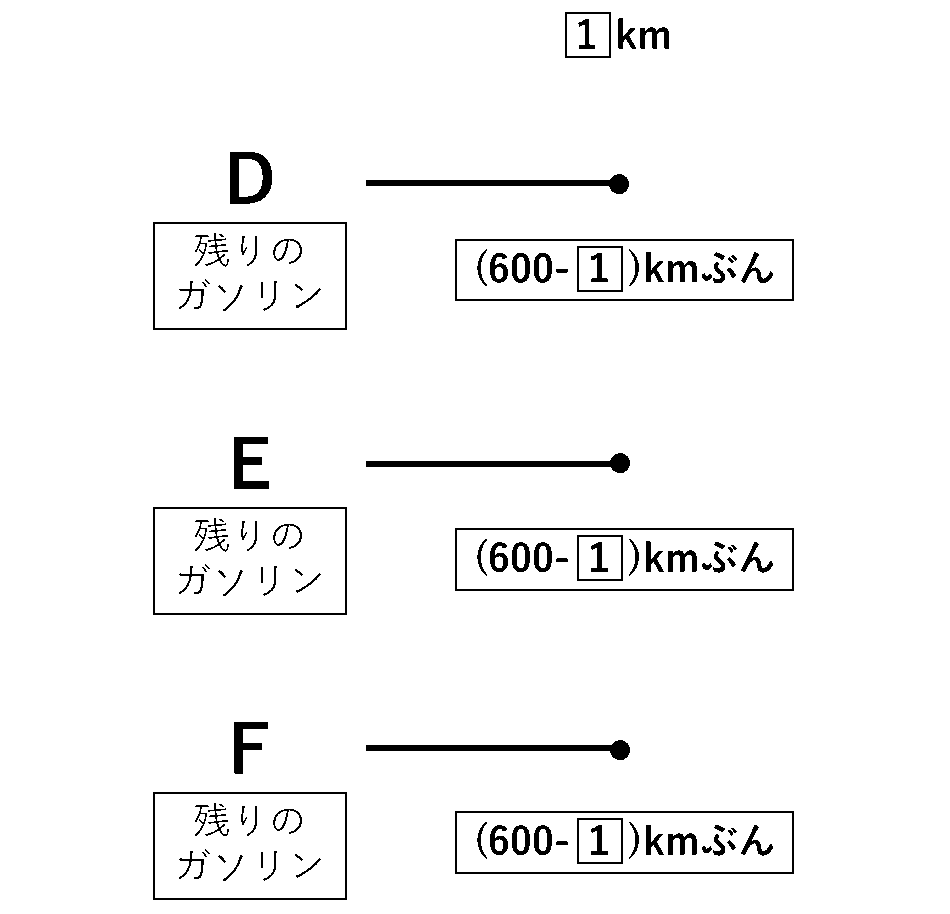 図5
図5
このとき,EとFの燃料タンクは満タンになるはずで,そのためには合計であと1×2=2(km)ぶんのガソリンを入れないといけませんので,この量がDの残りのガソリンと同じ量になります。だから,600-1=2です。これを解いて,1=200です。
EとFが200km移動したあと,さらに1km移動したときにもう1度ガソリンを移すとします。このとき,E,Fにはそれぞれ(600-1)kmぶんのガソリンが残っています。ここまでの状況を図にすると下の図6のようになります。
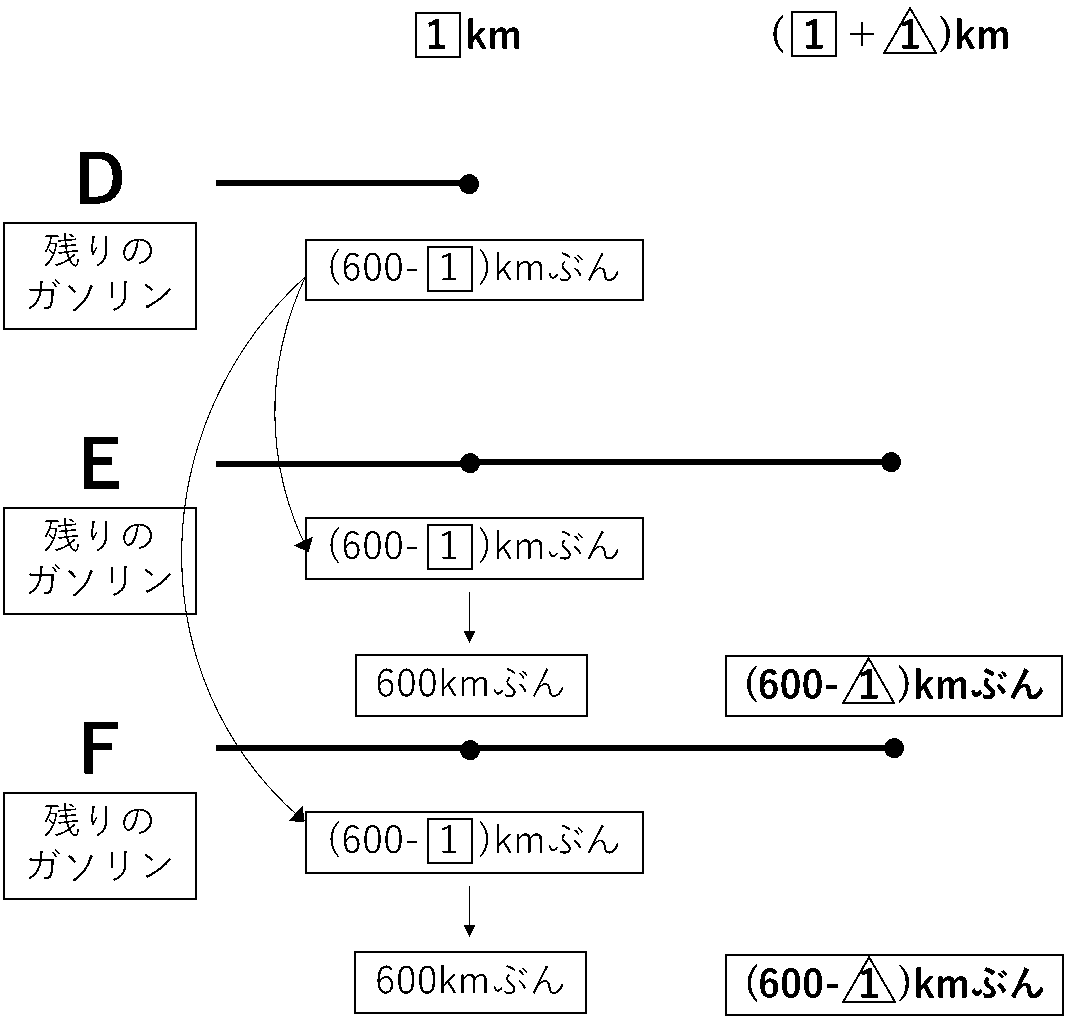 図6
図6
このとき,Fの燃料タンクは満タンになるはずで,そのためにはあと1kmぶんのガソリンを入れないといけませんので,この量がEの残りのガソリンと同じ量になります。だから,600-1=1です。これを解いて,1=300です。
Fは200km移動したあと300km移動して,さらに600km移動するので,答えは200+300+600=1100(km)です。
(3) (2)と同じように考えると,1番遠くまで移動する車は車が4台のとき最大1250km,車が5台のとき最大1370km,車が6台のとき最大1470kmまで移動できます。だから,答えは6台です。