わかるところは確定させることと，可能性が少ないところは場合分けすることを意識すると解きやすいです。

(1) 「もも」は全員が書いたので0点，「かき」はA君とB君の2人が書いたので1点，「りんご」はA君とC君の2人が書いたので1点，「みかん」はA君1人だけが書いたので2点，「れもん」もA君1人だけが書いたので2点です。
だから，A君の点数は0＋1＋1＋2＋2＝6（点）です。

(2) 2回目のゲームで1人だけが書いた単語はないので，2人が書いた単語の個数をd個，全員が書いた単語の個数をe個とすると，3人が書いた単語の個数の合計は10個なので，2×d＋3×e＝10です。この式を満たす整数d，eの組は，d＝5，e＝0とd＝2，e＝2です。
d＝2のとき，2つの2人が書いた単語を単語あと単語いとすると，単語あと単語いの書かれ方には次の2通りがあります。
<1> 2人がそれぞれ単語あと単語いの両方を書いている
<2> 1人が単語あと単語いの両方を，1人が単語あだけを，残りの1人が単語いだけを書いている
<1>と<2>の状況を絵にすると，下のようになります。

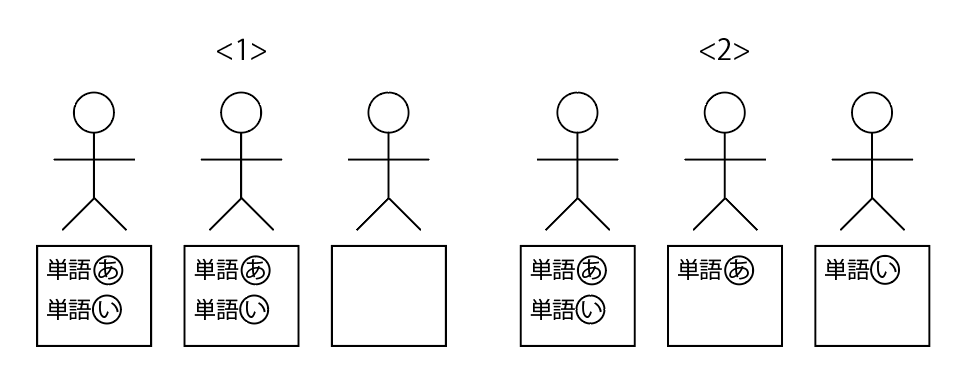
全員が書いた単語は0点なので，<1>の場合3人の点数は2点と2点と0点，<2>の場合3人の点数は2点と1点と1点で，どちらの場合も点数が同じ人がいます。だから，d＝2，e＝2だとおかしいです。
d＝5のとき，2人が書いた単語は書いた2人に1点ずつ，合計で2点与えられます。全員が書いた単語は0点なので，3人の点数の合計は2×5＝10（点）です。
（d＝5，e＝0のとき，たとえば2人が書いた5つの単語のうちA君とB君が書いた単語が3つ，A君とC君が書いた単語が2つあるとき，A君は5点，B君は3点，C君は2点になって3人の点数は異なります。また，また3人の書いた単語の個数は多い順にA君，B君，C君となります。）

(3) 3回目のゲームでC君が書いた単語のうち，C君だけが書いた単語，2人が書いた単語，全員が書いた単語の個数をそれぞれf個，g個，h個とします。このとき，C君は7個の単語を書いたので，f＋g＋h＝7…①です。また，C君は11点とったので，f×2＋g＝11…②です。②の式を満たす整数の組は，f＝5，g＝1とf＝4，g＝3とf＝3，g＝5とf＝2，g＝7とf＝1，g＝9とf＝0，g＝11の6組あります。①も成り立つようにすると，整数f，g，hの組としてありうるのは，f＝5，g＝1，h＝1とf＝4，g＝3，h＝0の2組です。
ここで，A君が書いた単語のうちA君だけが書いた単語の個数，2人が書いた単語の個数をそれぞれi個，j個とし，B君が書いた単語のうちB君だけが書いた単語の個数，2人が書いた単語の個数をそれぞれk個，m個とします。Aくんが書いた単語のうち全員が書いた単語の個数は，C君が書いた単語のうちの全員が書いた単語の個数と同じで，h個です。Bくんが書いた単語のうち全員が書いた単語の個数も，h個です。
A君，B君，C君の書いた単語の中にそれぞれ自分1人だけが書いた単語，2人が書いた単語，全員が書いた単語がいくつあるかをまとめて表にすると，下のようになります。


A君は9個の単語を答えたので，i＋j＋h＝9…③です。また，問題文の条件から，書いた単語の個数は多い順にA君，B君，C君です。A君は9個，C君は7個の単語を書いたので，B君は8個の単語を書いています。だから，k＋m＋h＝8…④です。また，C君が11点とって1位で，A君は3位なので，A君の点数は9点以下です。だから，2×i＋j≦9…⑤です。

fとgとhの値で場合分けをして考えます。
<1> f＝5，g＝1，h＝1の場合
③とh＝1から，i＋j＝8…⑥です。このことから2×i＋j＝i＋(i＋j)＝i＋8なので，⑤からi＋8≦9です。つまりi≦1なので，iは0か1です。⑥からi＋j＝8なので，iとjの値の組としてありうるのはi＝0，j＝8とi＝1，j＝7です。また，④とh＝1から，k＋m＝7…⑦です。
iとjの値で場合分けをして考えます。
[1]i＝0，j＝8の場合
A君が2×0＋1×8＝8（点）とって3位で，C君が11点とって1位なので，B君のとった点数は9点か10点です。だから，2×k＋m＝（9か10）…⑧です。⑧の両辺から⑦の両辺を引いて，k＝（2か3）です。⑦からk＋m＝7なので，m＝（4か5）です。
ここで，2人が書いた単語のうち，A君とB君が書いた単語の個数をn個，A君とC君が書いた単語の個数をo個，B君とC君が書いた単語の個数をp個とすると，n＋o＝8…⑨，n＋p＝m…⑩，o＋p＝1…⑪です。⑩の両辺と⑪の両辺を足すと，n＋o＋p×2＝m＋1…⑫です。このとき，⑫の両辺から⑨の両辺を引くと，左辺はp×2となりますが，右辺はm＋1つまり5か6から8を引くことになって引けません。だから，i＝0，j＝8だとするとおかしく，i=0，j=8ではありません。
[2]i＝1，j＝7の場合
A君が2×1＋1×7＝9（点）とって3位で，C君が11点とって1位なので，B君のとった点数は10点です。だから，2×k＋m＝10…⑬です。⑬の両辺から⑦の両辺を引いて，k＝3です。⑦からk＋m＝7なので，m＝4です。
ここで[1]と同じように，2人が書いた単語のうち，A君とB君が書いた単語の数をn個，A君とC君が書いた単語の数をo個，B君とC君が書いた単語の数をp個とすると，n＋o＝7…⑭，n＋p＝4…⑮，o＋p＝1…⑯です。⑮の両辺と⑯の両辺を足すと，n＋o＋p×2＝5…⑰です。このとき，⑰の両辺から⑭の両辺を引くと，左辺はp×2となりますが，右辺は5から7を引くことになって引けません。だから，i=1，j=7だとするとおかしく，i=1，j=7ではありません。
[1]，[2]から，f=5，g=1，h=1ではありません。

<2> f=4，g=3，h=0の場合
③とh＝0から，i＋j＝9…⑱です。このことから2×i＋j＝i＋(i＋j)＝i＋9なので，⑤からi＋9≦9です。つまりi≦0なので，iは0です。⑱からi＋j＝9なので，j＝9です。また，④とh＝0から，k＋m＝8…⑲です。A君が2×0＋1×9＝9（点）とって3位で，C君が11点とって1位なので，B君のとった点数は10点です。だから，2×k＋m＝10…⑳です。⑳の両辺から⑲の両辺を引いて，k＝2です。⑲からk＋m＝8なので，m＝6です。
ここで，<1>の[1]と[2]と同じように，2人が書いた単語のうち，A君とB君が書いた単語の数をn個，A君とC君が書いた単語の数をo個，B君とC君が書いた単語の数をp個とすると，n＋o＝9…㉑，n＋p＝6…㉒，o＋p＝3…㉓です。㉒の両辺と㉓の両辺を足すと，n＋o＋p×2＝9…㉔です。㉔の両辺から㉑の両辺を引くと，p×2＝0なのでp＝0です。このことと㉒，㉓から，n＝6，o＝3です。
ここまでのことから，上述の表の欄に数をうめると，下のようになります。


この表から，答えは2×0＋1×9＝9（点）です。