
算数オリンピックも感心!中学入試問題を紹介!
~メダリストはこう解く~

<問題11>
駒場東邦 2020年
赤,青,黄,白の長方形の紙が1枚ずつあり,それぞれのとなりあう2辺の長さは表のようになっています。この4枚を一部が重なるようにして図のように並べて1つの正方形を作ったとき,見えている部分の面積が4色すべて等しくなりました。このとき,次の問いに答えなさい。
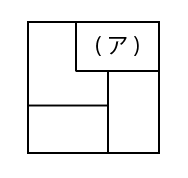
(2) 図の並べ方について,紙の色を下から順に答えなさい。
(3) 紙の並べ方を図と変えて,図と同じ大きさの正方形を作ったところ,見えている部分の面積は,青が105.6cm2,黄が156cm2になりました。この並べ方について,紙の色を下から順に答えなさい。また,赤の見えている部分の面積を求めなさい。
※中学校の許可を得て掲載しています。
<解答>
(1) 青色,24cm
(2) 赤,白,黄,青
(3) 赤,黄,青,白 , 122.4cm2
<解説>
わかるところをどんどん探して確定させていくことと,必要なときは場合分けをすることを意識すると,解きやすいです。
(3)は「あてはめ」に頼る解法しか思いつかず,論理的に解く方法は思いつきませんでした。
4枚の紙の面積は,赤が20×18=360(cm2),青が18×8=144(cm2),黄が20×9=180(cm2),白が20×9.6=192(cm2)です。
(1) (ア)が赤の紙だとします。このとき,(ア)の紙の見えている部分の面積は赤の紙全体の面積の360cm2なのに,青の紙全体の面積は144cm2なので青の紙の見えている部分の面積は144cm2以下です。しかし,見えている部分の面積は4色全部同じなので,これはおかしいです。だから,(ア)は赤の紙ではありません。同じように考えて,(ア)は黄色の紙でも白の紙でもありません。だから,(ア)の紙の色は青色です。
青の紙は1番上にあるので,青の紙の見えている部分の面積は青の紙全体の面積144cm2です。このことと見えている部分の面積が4色全部同じことから,[図]の正方形の面積は144×4=576(cm2)です。24×24=576から,面積が576cm2の正方形の1辺の長さは24cmなので,[図]の正方形の1辺の長さは24cmです。
(2) [図]の各頂点とそれぞれの紙に図1のように名前をつけます。
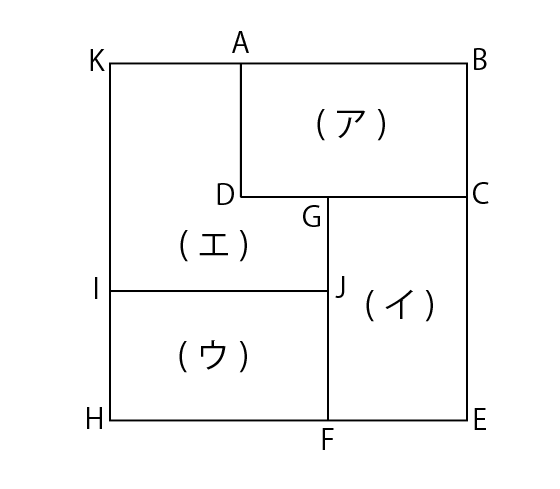 図1
図1
(ア)は青の紙なので,AB=18cm,BC=8cmです。また,四角形BEHKは1辺の長さが24cmの正方形なので,BE=24cm…①,EH=24cm…②,HK=24cm…③です。①とBC=8cmであることから,CE=BE-BC=24-8=16(cm)です。
また,(イ)の紙の見えている部分の面積は(ア)の見えている部分の面積と同じで144cm2なので,長方形CEFGの面積は144cm2です。だから,EFの長さは長方形CEFGの面積をCEで割って144÷16=9(cm)です。このことと②から,FH=EH-EF=24-9=15(cm)です。
また,(ウ)の紙の見えている部分の面積は(ア)の見えている部分の面積と同じで144cm2なので,長方形FHIJの面積は144cm2です。だから,HIの長さは長方形FHIJの面積をFHで割って144÷15=9.6(cm)です。このことと③から,IK=HK-HI=24-9.6=14.4(cm)です。
ここまでの状況を図に書くと,図2のようになります。
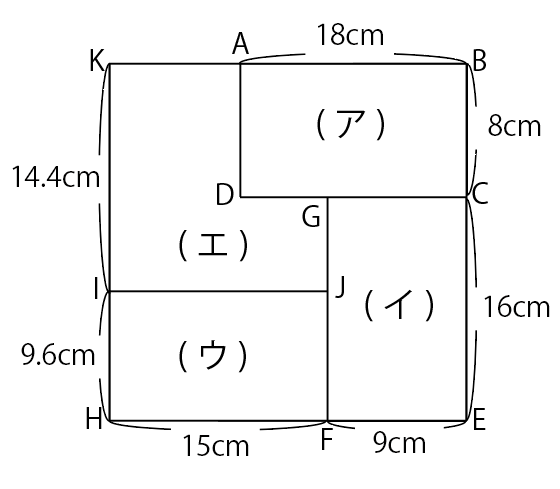 図2
図2
[図]の状態から(ア)の紙を取り除くと,図3または図4のような状態になります。
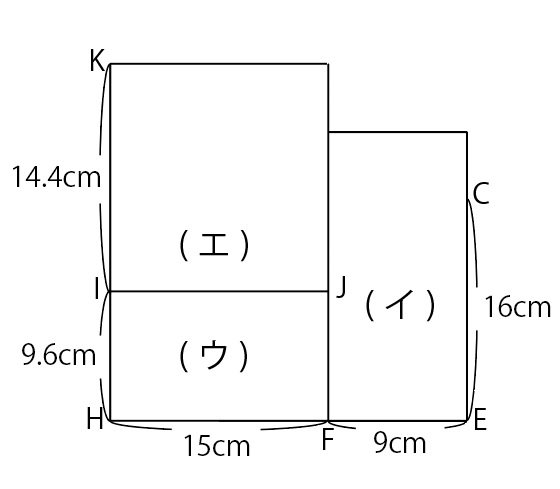 図3
図3
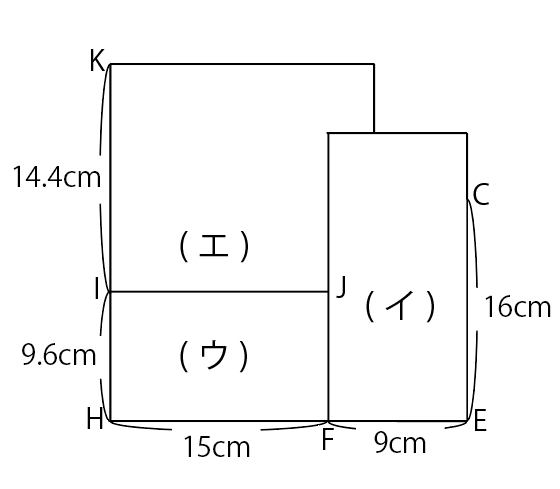 図4
図4
このとき,(エ)の紙について考えると,KIが14.4cmで,IJがFHと同じで15cmなので,(エ)の1辺は14.4cm以上で,もう片方の辺は15cm以上です。残っている赤の紙と黄色の紙と白の紙の中でこの条件を満たすのは赤の紙しかないので,(エ)は赤の紙です。このとき,図3の図だと赤の紙の辺の長さの片方は15cmということになってしまうので,図3はまちがいです。だから,正しい図は図4です。
(ウ)の紙について考えると,FHが15cmで,HIが9.6cmなので,(ウ)の1辺は15cm以上で,もう片方の辺は9.6cm以上です。残っている黄色の紙と白の紙のうちこの条件を満たすのは白の紙なので,(ウ)は白の紙です。だから,残った(イ)は黄色の紙です。
ここまでの状況を図に書くと,図5のようになります。
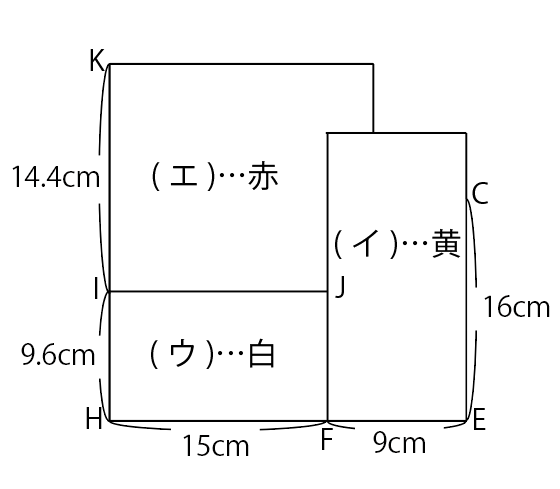 図5
図5
図5から,赤の紙は一部が別の紙でおおわれていて,1番上にはないことがわかります。また,白の紙もとなり合う2辺の長さはもともと20cmと9.6cmなので,図5から白の紙も一部が別の紙でおおわれていて,1番上にはないことがわかります。だから,図5で1番上にあるのは黄色の紙です。
図5の状態から黄色の紙を取り除くと,図6または図7または図8のような状態になります。
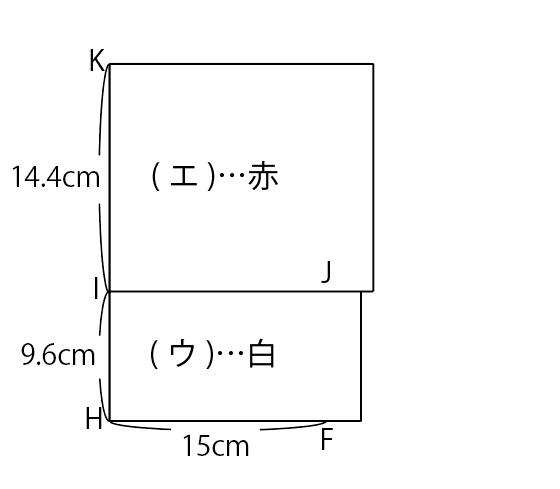 図6
図6
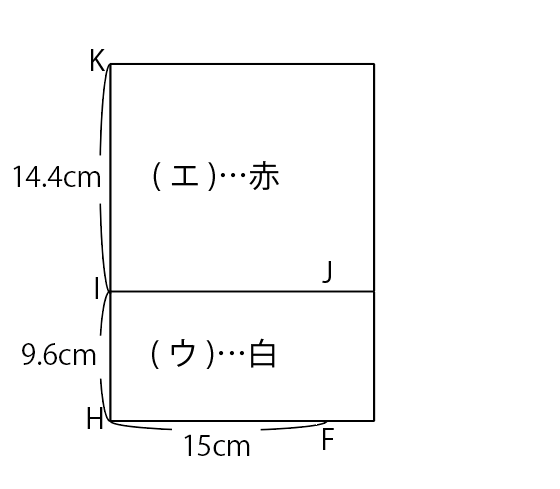 図7
図7
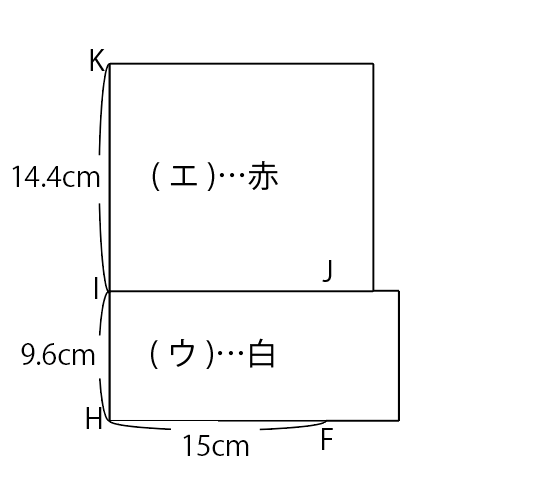 図8
図8
このとき,KIは14.4cmですが,赤の紙はとなり合う2辺の長さが20cmと18cmなので,赤の紙は白の紙に一部おおわれています。だから,赤の紙は白の紙より下にあります。
だから,答えは紙の色を下から順に答えて,赤,白,黄,青です。
(白の紙は9.6cmの辺を縦にして置いてあるので,白の紙の横の長さは20cmです。赤の紙が18cmの辺を縦にして置いてあったら,赤の紙の横の長さと白の紙の横の長さは両方とも20cmで同じなので,正しい図は図7です。赤の紙が20cmの辺を縦にして置いてあったら,赤の紙の横の長さは18cmで,白の紙の横の長さは20cmなので,正しい図は図8です。ただし,どちらが正しい図なのかは赤の紙がどちらの辺を縦にして置いてあるのかが分からないので,分かりません。)
(3) 1番上の紙の色が何か考えます。
1番上の紙は紙全体が見えているので,1番上の紙の面積と1番上の紙の見えている部分の面積は同じです。しかし,青の紙の見えている部分の面積は105.6cm2で,これは青の紙の面積とはちがうので,青の紙は1番上ではありません。同じように,黄色の紙も1番上ではありません。また,4枚の紙の見えている部分の面積の合計は1辺が24cmの正方形の面積と同じで,24×24=576(cm2)です。だから,赤の紙の見えている部分の面積と白の紙の見えている部分の面積を足すと576-105.6-156=314.4(cm2)…④です。
よって,赤の紙の見えている部分の面積は314.4cm2以下です。しかし,赤の紙の面積は360cm2です。つまり,赤の紙の面積と赤の紙の見えている部分の面積はちがうため,赤の紙は1番上ではありません。青の紙も黄色の紙も赤の紙も1番上ではないので,1番上にあるのは白の紙です。
このとき,白の紙の見えている部分の面積は白の紙の面積と同じで192cm2です。このことと④から,赤の紙の見えている部分の面積は314.4-192=122.4cm2です。
このことをもとに,いろいろ紙の重なり方を試すと,図9のように紙が重なっているとき問題の条件が満たされます。
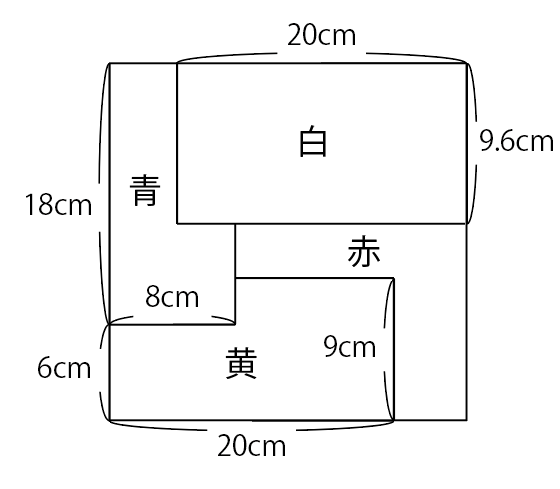 図9
図9
図9から,紙の色を下から順に答えると赤,黄,青,白です。
図9の考え方
赤の紙はおおわれている面積が360-122.4=237.6(cm2)と大きいので,赤の紙は1番下にあると考えられます。
青の紙の別の紙におおわれている部分の面積は144-105.6=38.4(cm2)です。これはとなり合う2辺の長さが9.6cmと4cmの長方形の面積に等しいです。だから,青の紙の上にとなり合う2辺の長さが9.6cmと4cmの長方形があるということは,青の紙の上に9.6cmの辺がある紙,つまり白の紙があるかもしれません。
同じように考えて,黄色の紙の別の紙におおわれている部分の面積は180-156=24(cm2)です。これはとなり合う2辺の長さが8cmと3cmの長方形の面積に等しいです。だから,黄色の紙の上にとなり合う2辺の長さが8cmと3cmの長方形があるということは,黄色の紙の上に8cmの辺がある紙,つまり青の紙があるかもしれません。
このように考えると,早く答えを見つけることができます。