＜広中杯＞
問題Ⅰ-(4)　 nの最小の値

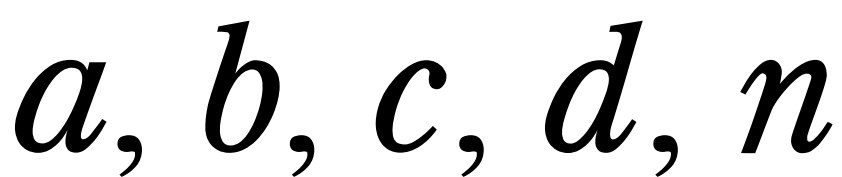正の整数は

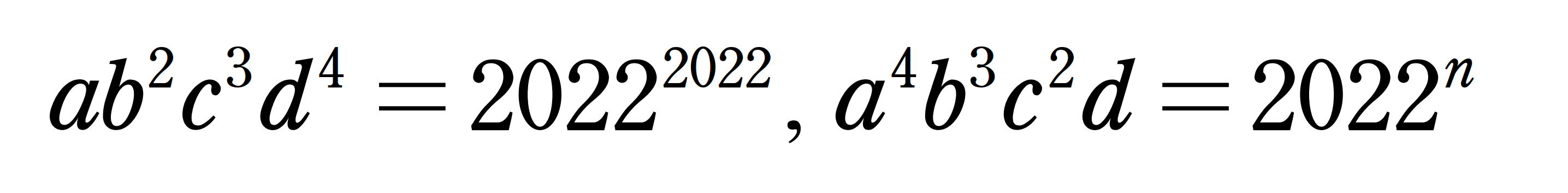
を満たしている。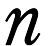として考えられる最小の値を求めよ。

（正答率：33.3%）

＜解答＞

５０８

＜講評・ワンポイントアドバイス＞

2022を素因数分解して、あれこれと組み合わせを試したくなりますが、色んなパターンが考えられるので混乱してしまいますね。細かな処理にこだわりすぎずに、ざっくりと大きな視点で数式を眺めることがポイントだったのではないでしょうか。

指数が1,2,3,4と4,3,2,1という風に対称的になっています。　※ 対称性に着目！
だから２つの与式をかけあわせると　a5b5c5d5＝20222022+n となります。
これだけでかなり見通しが良くなりますね。

つまり abcd＝2022(2022+n)/5 です。
よって 2022＋n は５で割り切れるはずだから n＝3＋(5の倍数) ですね。
では n=3 が最小なのか。
いやいやさすがに小さすぎる。
他に条件がありそう。

そもそもabcd＝2022(2022+n)/5で a4b3c2d＝2022nということは
(2022+n)/5 ≦ n なのだからn > 505だとわかりますね。
n > 505 かつ n＝3＋(5の倍数) より、最小のnは508

「木を見て森を見ず」ではなく、まずは森を遠くからゆっくり眺めてみましょう。