＜算数オリンピック＞
問題7　正方形⇒長方形

マス目の間かくが１mmの方眼紙の方眼の線にそって、長方形を作りました。
そして、次のルールにしたがって、長方形から正方形を作りました。

＜ルール＞
①方眼の線にそって、２段以上の階段状の形AとBに切りはなす。

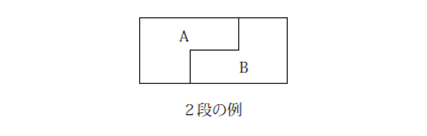
②Aを右上にずらして、Bとぴったりつなぎ合わせて１つの正方形を作る。

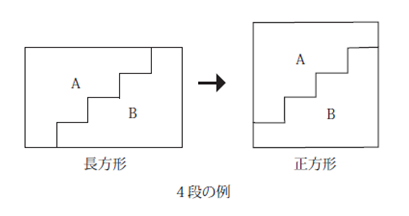
できた正方形の一辺の長さが72mmになるとき、もとの長方形のまわりの長さは何mmですか。 ３通り答えなさい。

（正答率：27.1%）

（ファイナリスト正答率：80.5%）

＜解答＞

290mm, 300mm, 312mm

＜講評・ワンポイントアドバイス＞

条件はすごくシンプルですが、なんだか掴み所のない(初めて見る)問題なので、イヤですね。 戸惑った人も多かったと思います。
4段の例が与えられているので、その図から問題特性をきちんと把握できるかどうかが大きな分かれ目になりますね。

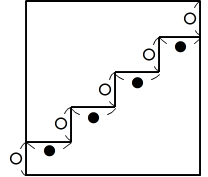
例えば4段では右図のように●(横)よりも〇(たて)が1個多い。
2段の正方形で考えても同じように●(横)よりも〇(たて)が1個多い。

●と〇は整数だから，結局は
72の約数(1,2,3,4,6,8,9,12,18,24,36,72)のうち連続しているペア、つまり●と〇の個数の組合せは(●,〇)＝(1,2), (2,3), (3,4), (8,9) があてはまります。
※ ただし (1,2) は1段になってしまうので不適。

一見すると図形問題だけど、実は整数問題というオチ。
全体正答率27.1%に対して、ファイナリストの正答率は80.5%と、かなり大きな差がついています。
初めて見るような問題では「う～ん…。どうしようかな…」と悩むことは避けられませんが、その前に「調べる・試す」ことです。
そうすれば視界がクリアになって「なんだ。それだけのことか。」となることもよくありますから。