＜広中杯＞
Ⅱ-(４)　セブンな数

284や7777のように、どの隣り合う２桁の部分を取り出し、それを２桁の正の整数と解釈しても、それが必ず７の倍数となっているような、どの桁の数字も０ではない２桁以上の正の整数を、「セブンな数」ということにする。
　20桁のセブンな数は全部でいくつあるか。

（正答率：28.0%）

＜解答＞

32772個

＜講評・ワンポイントアドバイス＞

模範解説のようにスマートに解けることが理想的ですが、ここではひとつ別解を示します。

まず２桁の数を置いて、その右隣に題意を満たす３桁目に置く。
その右隣に題意を満たす４桁目に置く。… と繰り返すので、一の位に着目。

２桁の７の倍数のうち０を含まないものを一の位の数でグループ分けすると以下。
① 21,91, ② 42, ③ 63, ④ 14, 84, ⑤ 35, ⑥ 56, ⑦ 77, ⑧ 28, 98, ⑨ 49

中学受験でおなじみのフィボナッチ的な解法(漸化式的な解法)を適用すると次の表になる。

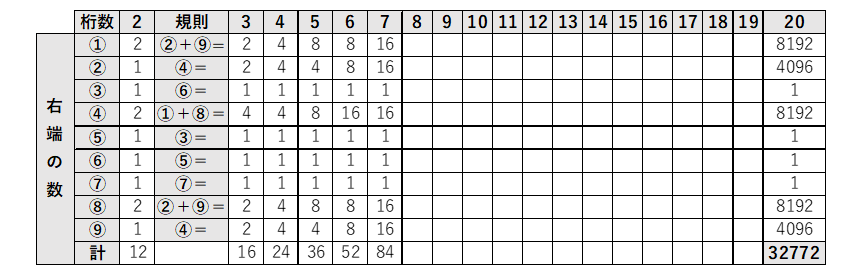
※ ３桁以降は「規則」に従って埋めていく。８桁～19桁は省略。
※ ①,②,④,⑧,⑨において２の累乗数の規則性を利用すれば途中は省エネ可能。

模範解説とともに参考にして下さい。上の解法はあまり実戦的とは言えませんが、論理の根本を理解する手助けになれば幸いです。