＜ジュニア算数オリンピック＞
問題9　台形の面積

図のように、正三角形１つと正方形２つと二等辺三角形１つを組み合わせて図形を作りました。
PQ＝１cmのとき、太線部分の面積を求めなさい

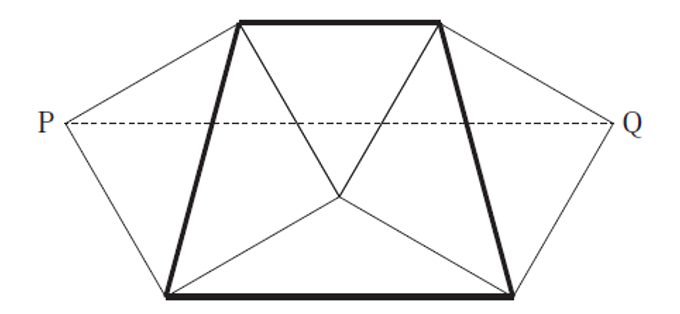
（正答率：17.7%）

＜解答＞

0.25cm2

＜講評・ワンポイントアドバイス＞

模範解説では図のように等積移動を利用しています。解説を見れば「なんだ。これだけのことか…。」とあっけなく見えますね。でも実際に問題を前にすると、そう簡単には気づけないものです。

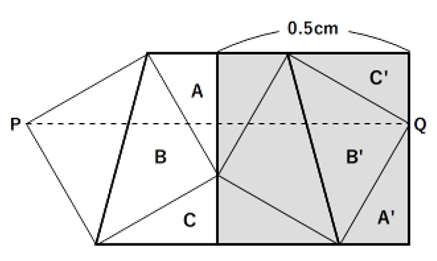
こういう問題に強くなるためにはどうすべきか。
⇒ 何時間でも何日でも(何週間でも!?)時間をかけていい。自力で解法を見つけること。
　 ※ 問題を覚えて頭の中だけで、いつでもスキマ時間にあれこれと考えられるように。
　 ※ 解説を見てしまった場合は別解を考えてみましょう。この問題にも多くの別解があります。

見た目は異なりますが、豊島岡女子学園2024で類題が出題されています。

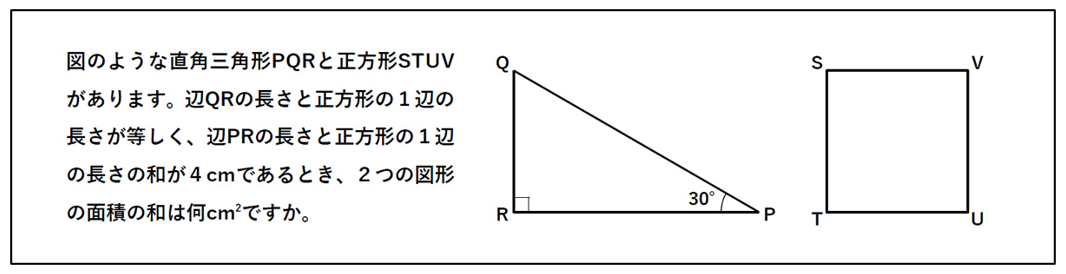
※ 解説は みんなの算数オンライン https://www.min-san.com/dbz/ps/1/66c574e5caf85/0/

最難関校の豊島岡女子学園でも正答率は20%ほどですから、中学受験的には相当な難問という評価になります。ですからジュニアで正答率17.7%は立派ですね。