＜算数オリンピック＞
問題5　素数の和

下の９マスに、100以下の異なる素数を１つずつ入れます。
丸の中の数は、周りの４つのマスの数字の和を表します。
すべてのマス目に数字を書き入れなさい。
ただし、100以下の素数は次の25個です。
２、３、５、７、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、 97

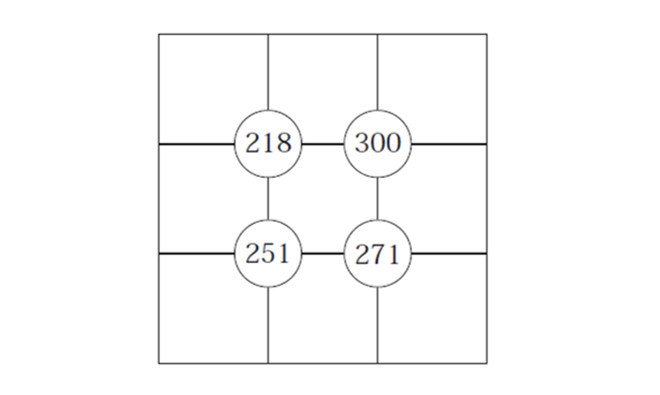
（正答率：31.9%）

＜解答＞

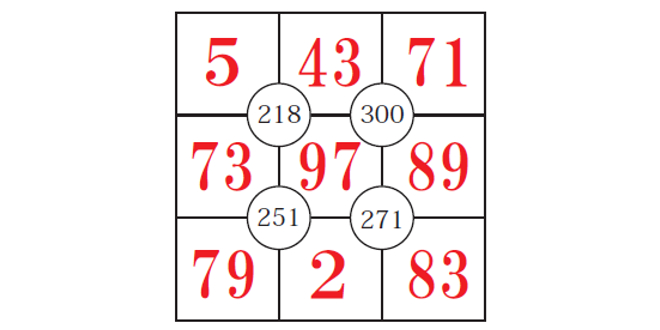
＜講評・ワンポイントアドバイス＞

この手の問題では「数の大きさ」に着目するのが一般的なアプローチですが、最小の218や最大の300について考えても候補が多くてなかなか絞り込めません。そこで「数の偶奇性」に目を向けてみましょう。

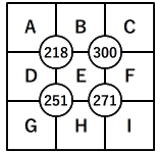
251と271は奇数。
⇒　４つの素数の和が奇数
⇒　４つとも奇数だと和は偶数になってしまうから、少なくとも１つは偶数のはず。
⇒　素数はほとんど奇数だけど、唯一２だけは偶数。
⇒　251と271が奇数で, 218と300は偶数ってことは…。どれが２だろうか…。
⇒ H＝２
⇒ E+F+I＝271－2＝269＝97+89+83
⇒　いろいろと当てはめて調べる。または論理的に埋めていく。(模範解説参照)

H＝2 に気付いた後も簡単ではない(むしろH=2に気付いてからの方が面倒かも…)ので、正答率31.9%(ざっくり３人に１人は正解)というのは想定を超えます。素晴らしい。

普段から「数の特徴」に敏感であること、そして泥臭く「探す」 「試す」 「調べる」という姿勢を忘れないで問題に臨んで下さい。