<結果発表!>
伊藤成希 さん
神奈川県 12歳
小学6年生
委員からのコメント:
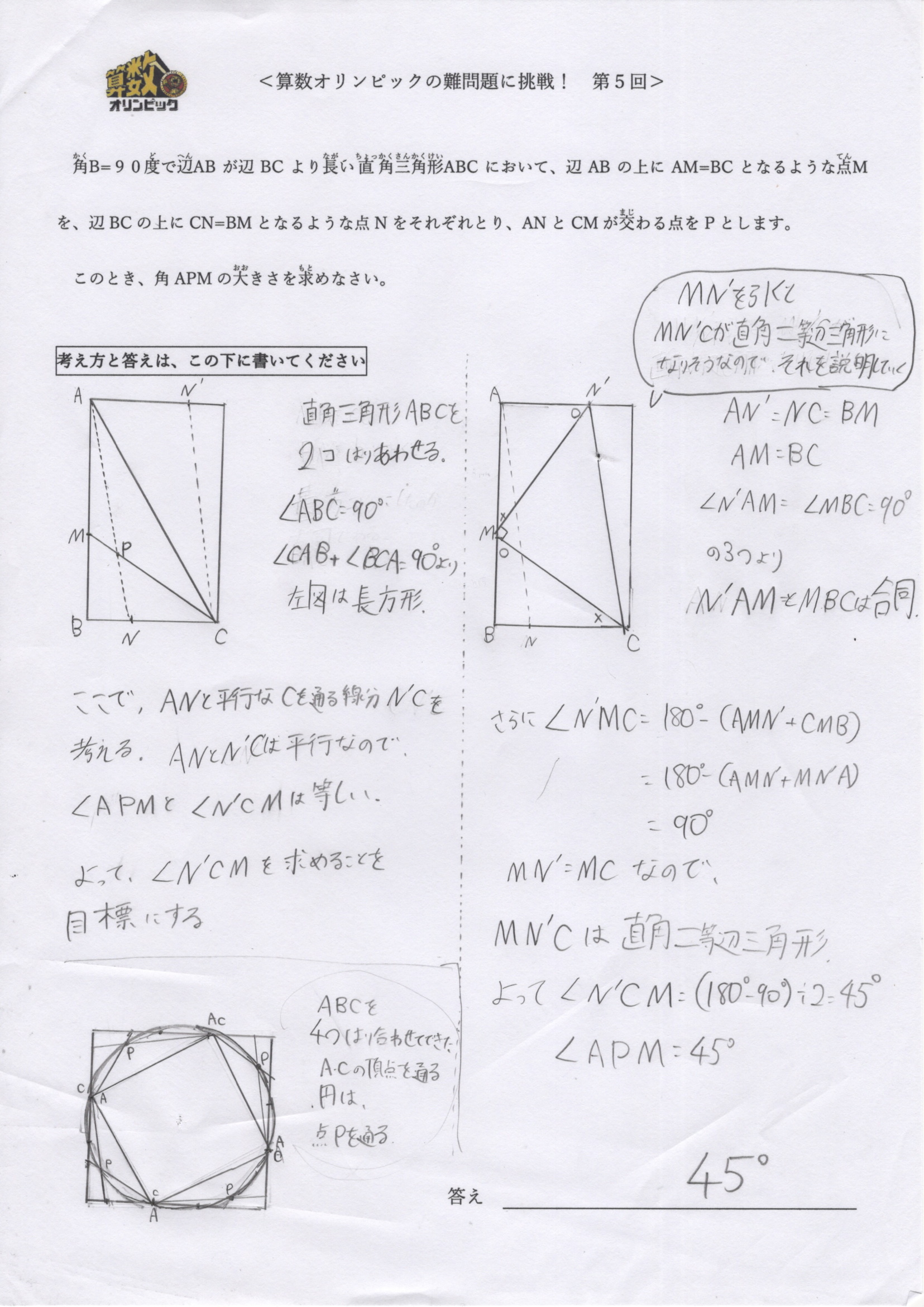
「直角三角形ABCを点対象に回転させて貼り合わせる考え方もすばらしかったのですが、角APMが八角形の外角になることを図示して表現したことはすばらしい着眼だと思います。
もう少し説明が欲しかったのですが、委員は180-135=45度かあ…と唸りました。」
「直角三角形ABCを2個貼り合わせた長方形に着目するというのはシンプルでわかりやすい☆
また円に内接する形を見せてくれたのも参考になります!」



委員からのコメント:
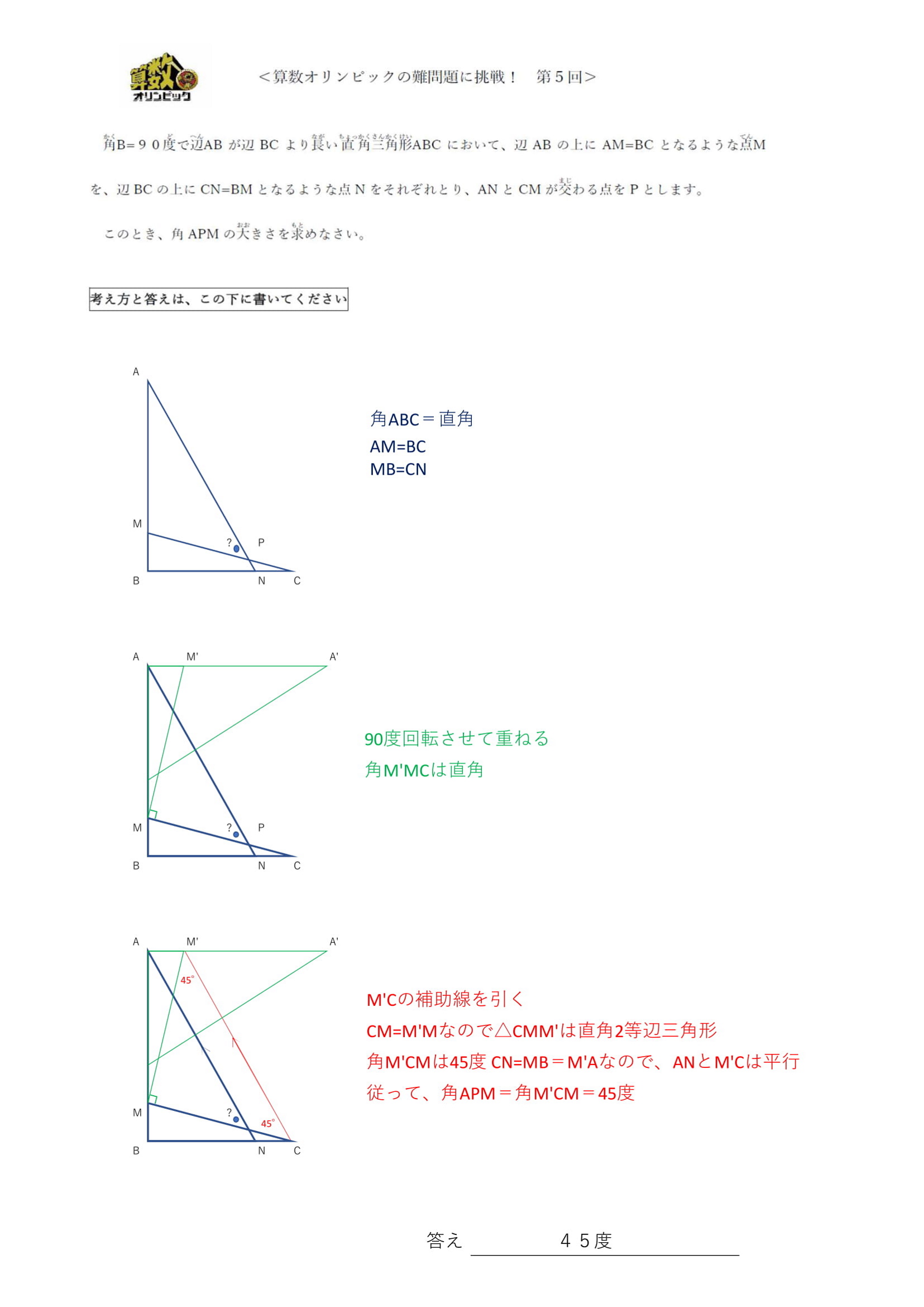
「アプローチの方法に感心しました。 Mが点Bに限りなく近い場合と、Mが点Aと点Bの中点に限りなく近い場合との、両方で仮定して考えてくれました。 この考え方は数学では重要な考え方ですが、この図形の問題で応用してくるかあ…と思わず感心しました」
「極端な場合、特に最長の場合と最短の場合で、どちらも図示してくれたのがとても良かったですね☆」