＜結果発表！＞
白圡奏佑 さん
千葉県 9歳
小学3年生
神無太郎 さん
静岡県 60歳
会社員
委員からのコメント：
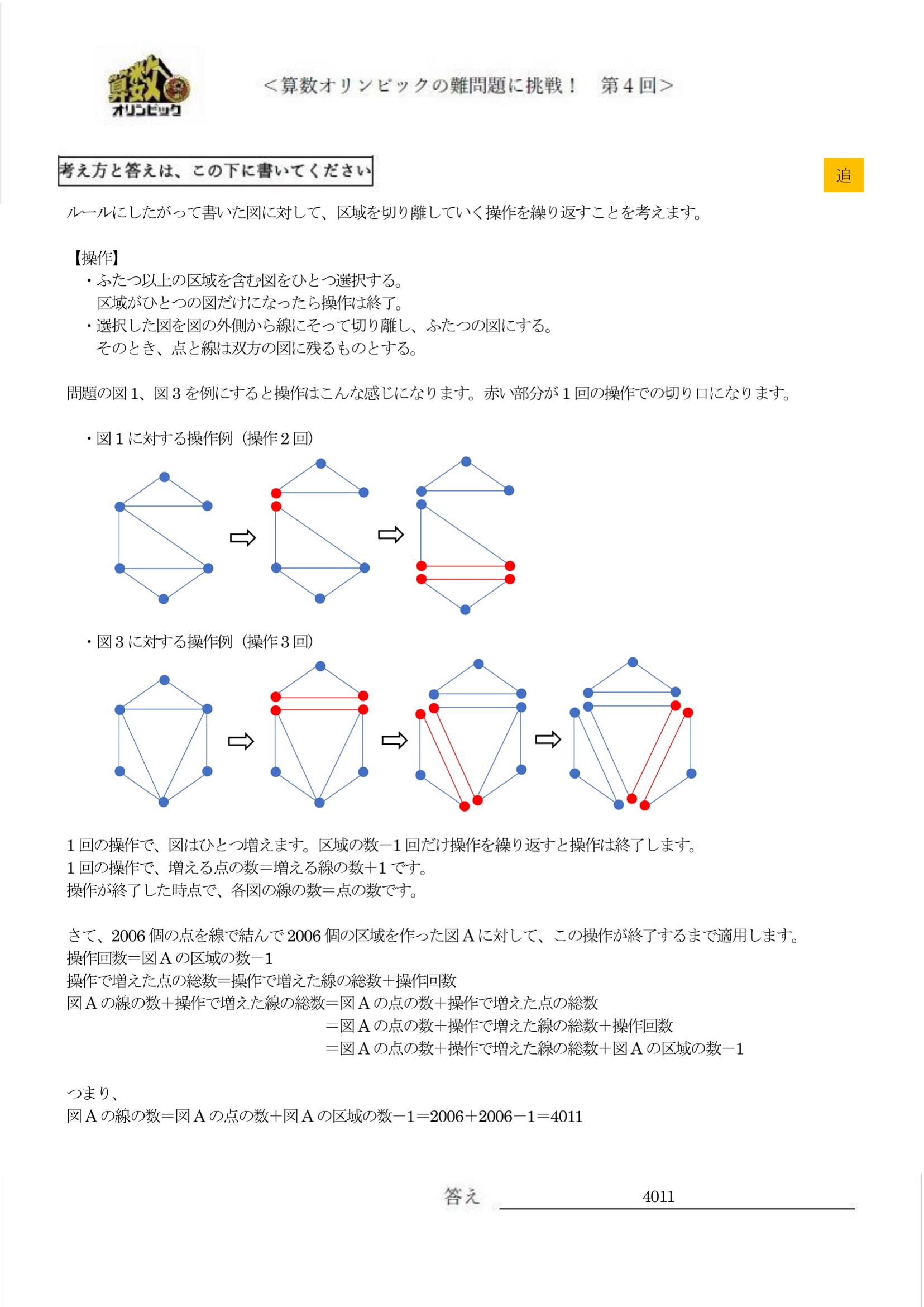
「今回のフリー部門はレベルの高い“考え方”が多く、選考に悩まされました。その中でも、問題自体を解剖し、“線の数=点の数+区域の数―1”という公式を導いてくれました。また、もしも区域を分離してもよいときはどのように考えるのかも提示して頂きました。この問題自体を解剖するという考え方は、“難問チャレンジ“に応募する小学生たちにぜひ伝えたいと思いました。」
「アプローチのパターンをそれぞれ詳細に示して頂きました。大変参考になりますね。」
「点・線を消す操作、区域を切り離す操作、というお考えに“おおっ”となりました。」
委員からのコメント：
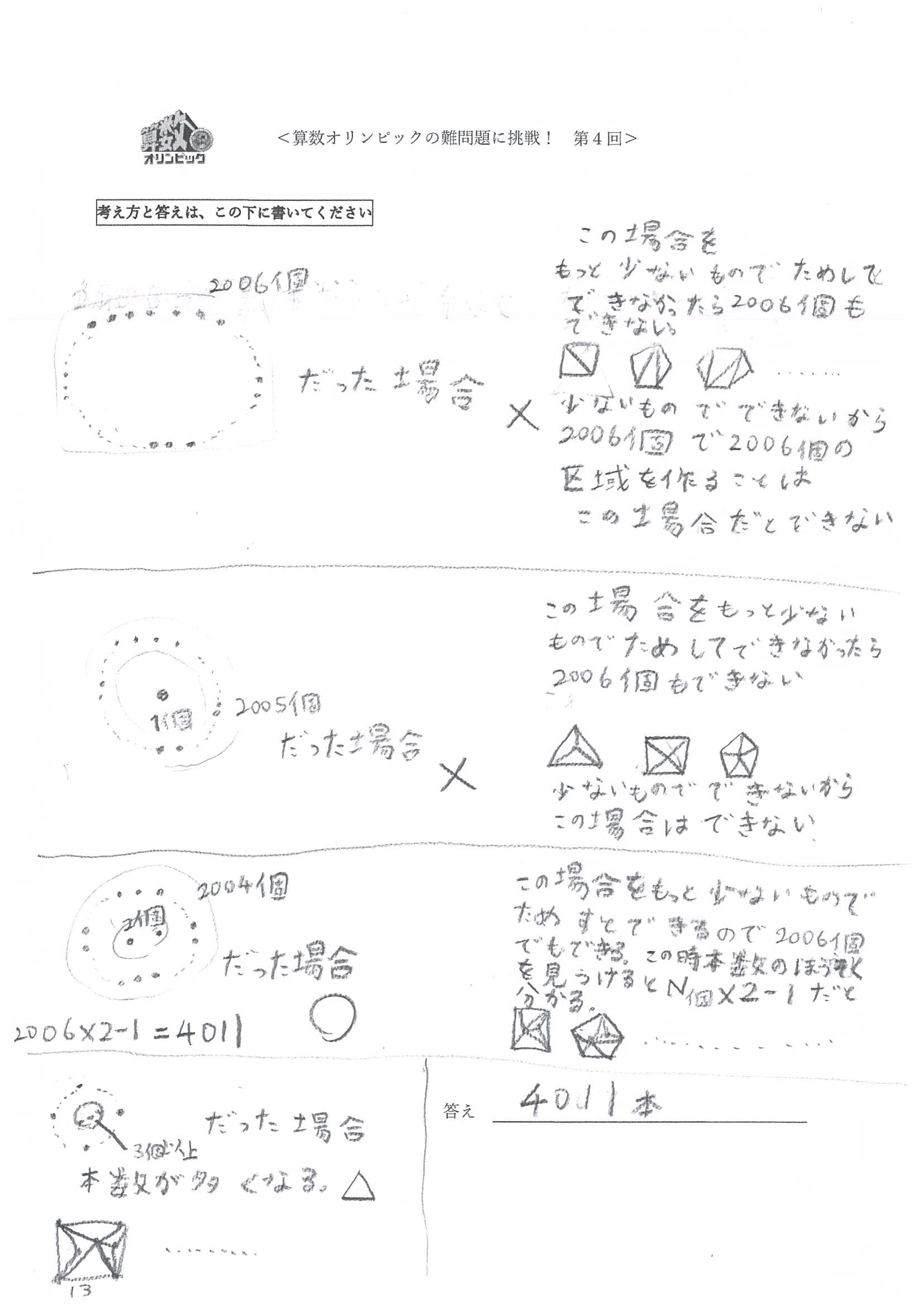
「全ての点を周上に打った場合というところから考えてきました。全ての点(2006個の点)が周上にある場合は条件の区域をつくることができないのですが、その内部に点を打ち、区域を広げていくという発想に“うーむ！”とうなりました。」
「外側の点をつなぐことで、内側の点の個数だけを考えていくという発想が素晴らしい！」
「内部の点が３個以上だった場合、本数が多くなるが成立する場合もある。それを△で表したこともいいですね。」