委員からのコメント：
「“168度→これを見たら正30角形が思いついた”“108度→168度との差が60度→正三角形があやしい”という発想が素敵ですね！問題の条件や出題の意図を見抜く力が素晴らしいです。」

「168度で正30角形が思いついた！という目の付け所がいい☆」

委員からのコメント：
「“四角形ABCDをずらして重ねてみる”“ずらして重ねた結果、正三角形と二等辺三角形が現れた”というアプローチには唸りました。委員はとても勉強になりました。」

「少しずらして合同な図形を作る。なかなか思いつかない一手ですね！」

委員からのコメント：
「⊿BCDを回転させて正五角形をつくる。結果として正三角形ができ、線対称の形になった。また、等脚台形や二等辺三角形も現れる、という全ての要素を満たしていました。」

「星型五角形を作ることで、正五角形や等脚台形まで色んな解法の基になる発想ですね！」

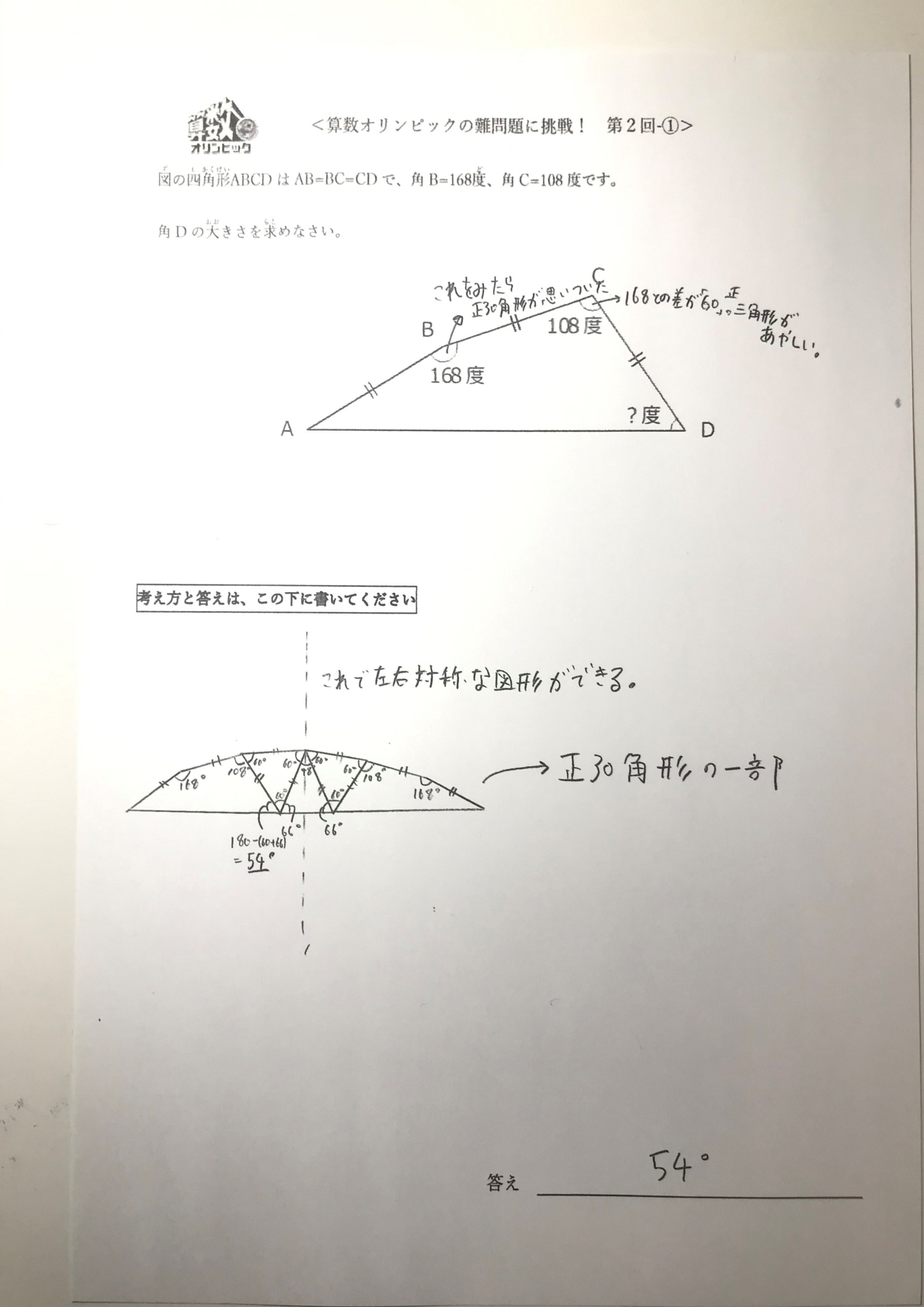
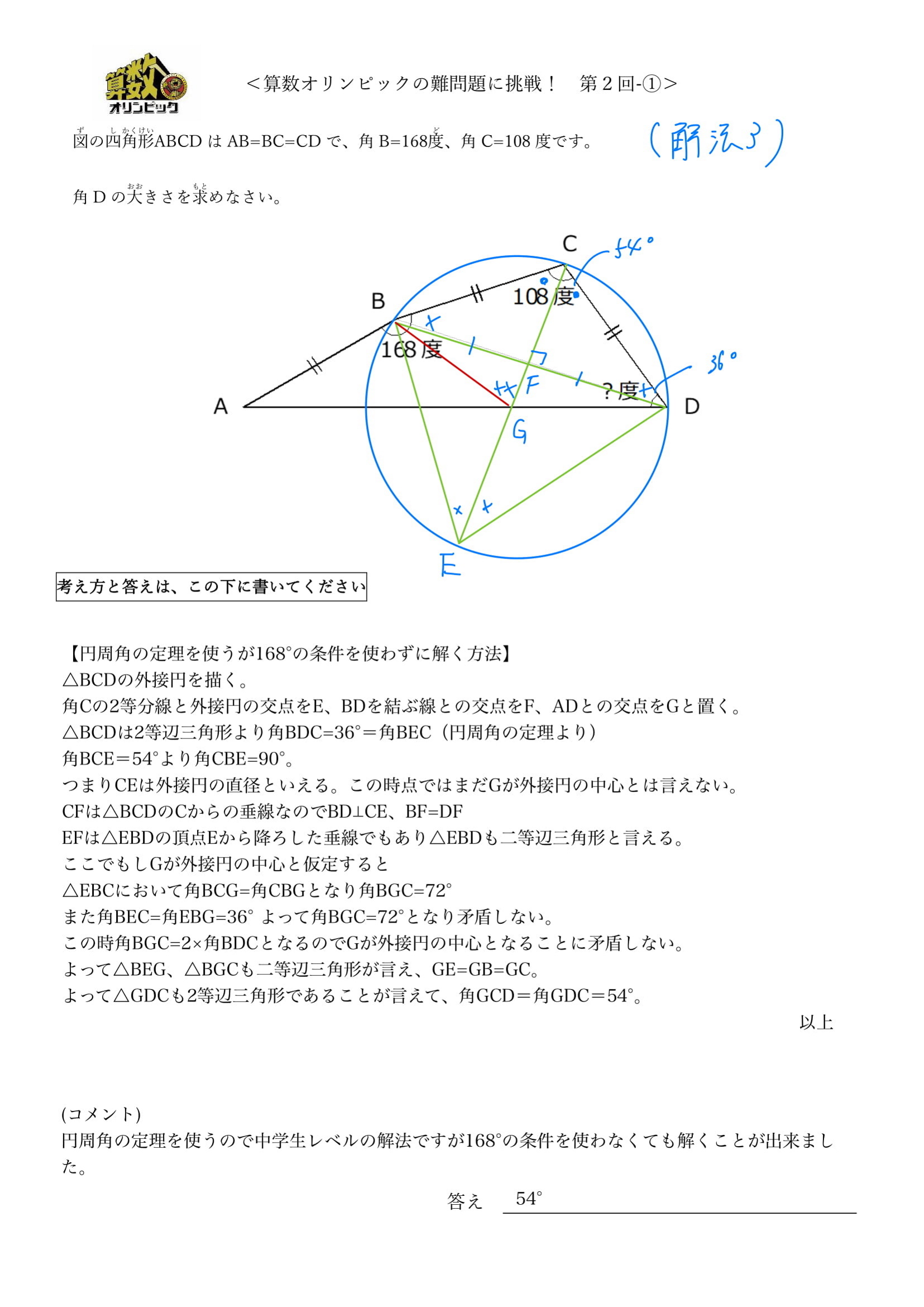
委員からのコメント：
「外接円の中心が辺AD上にあることや、168度の条件を使用しなくても問題が解けることを証明して頂きました。算数と数学の境目の世界を参加者に見せて頂き感謝です。」

「なるほど！円周角を利用すると168度を使わなくてもＯＫ。勉強になりますm(_ _)m」